题目内容
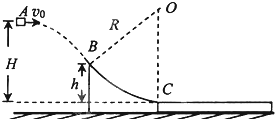
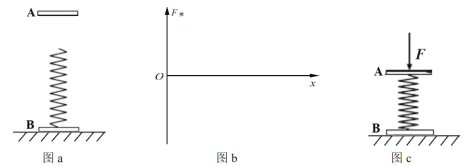
【题目】如图a所示，弹簧下端与静止在地面上的物块B相连，物块A从距弹簧上端H处由静止释放，并将弹簧压缩，弹簧形变始终在弹性限度内。已知A和B的质量分别为m1 和 m2，弹簧的劲度系数为k，重力加速度为g，不计空气阻力。取物块A刚接触弹簧时的位置为坐标原点O，竖直向下为正方向，建立 x 轴。
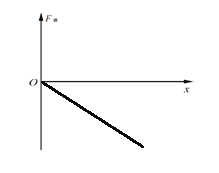
(1)在压缩弹簧的过程中，物块A所受弹簧弹力为F弹，请在图b中画出F弹 随x变化的示意图；并根据此图像，确定弹簧弹力做功的规律；
(2)求物块A在下落过程中最大速度vm 的大小；
(3)若用外力F将物块 A压住（A与弹簧栓接），如图c所示。撤去 F后，A 开始向上运动，要使B能够出现对地面无压力的情况，则F至少多大？
【答案】(1) 
,
；(2)
（3）
【解析】
(1)由胡克定律可得，A受到的弹力为
（x为A的位移即弹簧的形变量），所以弹力与x成正比，图像如图所示
A运动x的位移时的弹力为
由于弹力与位移成正比，所以弹力的平均值为
从A接触弹簧到A运动x的位移时，弹力所做的功为
(2)当物体的加速度为零时，速度最大，此时有
由动能定理得
解得：
(3) 用外力F将物块A压住时，弹簧的压缩量为
，此时由平衡可知
B刚好离开地面时弹簧的伸长量为
，由平衡可知
B刚好离开地面时A的速度为0，从撤去力F到B刚好离开地面由动能定理得
联立以上三式解得
练习册系列答案
相关题目
