题目内容
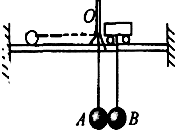 如图所示,质量为0.3kg的小车静止在光滑的轨道上,在它下面挂一个质量为0.1kg的小球B,车旁有一支架被固定在轨道上,支架上O点悬挂一质量也为0.1kg的小球A,两球的球心至悬挂点的距离均为0.2m.当两球静止时刚好相切,两球心位于同一水平线,两条悬线竖直且相互平行.若将A球向左拉至图中虚线所示位置后从静止释放,与B球发生碰撞,碰撞中无机械能损失,求碰后B球上升的最大高度.(重力加速度g=10m/s2)
如图所示,质量为0.3kg的小车静止在光滑的轨道上,在它下面挂一个质量为0.1kg的小球B,车旁有一支架被固定在轨道上,支架上O点悬挂一质量也为0.1kg的小球A,两球的球心至悬挂点的距离均为0.2m.当两球静止时刚好相切,两球心位于同一水平线,两条悬线竖直且相互平行.若将A球向左拉至图中虚线所示位置后从静止释放,与B球发生碰撞,碰撞中无机械能损失,求碰后B球上升的最大高度.(重力加速度g=10m/s2)分析:本题考查连接体碰撞问题,在小球下落过程中机械能守恒,求出A到达最低点时速度再由动量守恒定律、机械能守恒定律求出上升的高度.
解答:解:A球下落过程,由动能定理有 mAgl=
mAv12
AB碰撞后瞬间,B的速度v2=v1
对B和车系统,在水平方向有mBv2=(M+mB)v
由机械能守恒定律有
mBv22=
(M+mB) v2+mBgh.
解得 h=0.15m
答:碰后B球上升的最大高度是0.15m
| 1 |
| 2 |
AB碰撞后瞬间,B的速度v2=v1
对B和车系统,在水平方向有mBv2=(M+mB)v
由机械能守恒定律有
| 1 |
| 2 |
| 1 |
| 2 |
解得 h=0.15m
答:碰后B球上升的最大高度是0.15m
点评:该题是一道综合题,综合运用了机械能守恒定律、动量守恒定律、动能定理,解决本题的关键熟练这些定理、定律的运用

练习册系列答案
相关题目
 如图所示,质量为0.5kg的物块以5m/s的初速度从斜面顶端下滑,斜面长5m,倾角为37°,物块与斜面间的动摩擦因数μ=0.5.求:
如图所示,质量为0.5kg的物块以5m/s的初速度从斜面顶端下滑,斜面长5m,倾角为37°,物块与斜面间的动摩擦因数μ=0.5.求: 如图所示,质量为0.1kg的小球从竖立的轻质弹簧正上端C(状态甲)由静止自由下落到弹簧上端B(状态乙),B为弹簧处于自然状态的位置,A为弹簧压缩到的最低位置(状态丙).已知A、B的高度差为0.3m,B、C的高度差为0.5m,g=10m/s2.则下列说法正确的是( )
如图所示,质量为0.1kg的小球从竖立的轻质弹簧正上端C(状态甲)由静止自由下落到弹簧上端B(状态乙),B为弹簧处于自然状态的位置,A为弹簧压缩到的最低位置(状态丙).已知A、B的高度差为0.3m,B、C的高度差为0.5m,g=10m/s2.则下列说法正确的是( ) 如图所示,质量为0.5kg的小球,从桌面以上高1.2m的A点下落到地面的B点,已知桌面高0.8m,求:
如图所示,质量为0.5kg的小球,从桌面以上高1.2m的A点下落到地面的B点,已知桌面高0.8m,求: 如图所示,质量为0.2kg的物体带正电,其电量为4×10-4C,从半径为0.3m光滑的
如图所示,质量为0.2kg的物体带正电,其电量为4×10-4C,从半径为0.3m光滑的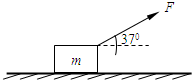 如图所示,质量为0.78kg的金属块放在水平桌面上,在与水平成37°角斜向上、大小为3.0N的拉力F作用下,以4.0m/s的速度向右做匀速直线运动.已知sin37°=0.60,cos37°=0.80,g取10m/s2.
如图所示,质量为0.78kg的金属块放在水平桌面上,在与水平成37°角斜向上、大小为3.0N的拉力F作用下,以4.0m/s的速度向右做匀速直线运动.已知sin37°=0.60,cos37°=0.80,g取10m/s2.