题目内容
 如图所示,小球质量为m,用两根轻绳BO、CO系好后,将绳固定在竖直墙上,在小球上加一个与水平方向夹角为60°的力F,使小球平衡时,两绳均伸直且夹角为60°.则力F的大小应满足什么条件?
如图所示,小球质量为m,用两根轻绳BO、CO系好后,将绳固定在竖直墙上,在小球上加一个与水平方向夹角为60°的力F,使小球平衡时,两绳均伸直且夹角为60°.则力F的大小应满足什么条件?分析:当力F最小时,OC绳松驰,张力为零;当力F最大时,OB绳松驰,张力为零.根据平衡条件分别求出力F的最小值和最大值,再求出力F的范围.
解答:解:当力F最小时,OC绳松驰,张力为零,此时小球受到三个力作用.设绳BC的拉力为T1,则由平衡条件得
mg=Tsin60°+F1sin60° ①
Tcos60°=F1cos60° ②
由②得T=F,代入①解得,F1=
mg
当力F最大时,OB绳松驰,张力为零,此时小球受到三个力如图,根据平衡条件得
F2=
=
mg
所以力F的大小应满足的条件是
mg≤F≤
mg
答:力F的大小应满足的条件是
mg≤F≤
mg.

mg=Tsin60°+F1sin60° ①
Tcos60°=F1cos60° ②
由②得T=F,代入①解得,F1=
| ||
| 3 |
当力F最大时,OB绳松驰,张力为零,此时小球受到三个力如图,根据平衡条件得
F2=
| mg |
| sin60° |
2
| ||
| 3 |
所以力F的大小应满足的条件是
| ||
| 3 |
2
| ||
| 3 |
答:力F的大小应满足的条件是
| ||
| 3 |
2
| ||
| 3 |
点评:本题是物体平衡中极值问题,也可以根据正交分解法,得到F与两个绳子拉力的关系式再求解范围.

练习册系列答案
相关题目
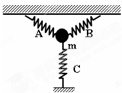 如图所示,小球质量为m,被三根质量不计的弹簧A、B、C拉住,弹簧间的夹角均为120°,小球平衡时,A、B、C的弹力大小之比为3:3:1,当剪断C瞬间,小球的加速度大小及方向可能为( )
如图所示,小球质量为m,被三根质量不计的弹簧A、B、C拉住,弹簧间的夹角均为120°,小球平衡时,A、B、C的弹力大小之比为3:3:1,当剪断C瞬间,小球的加速度大小及方向可能为( ) (2011?河南模拟)如图所示,小球质量为m,被三根质量不计的弹簧A、B、C拉住,弹簧间的夹角均为1200,小球平衡时,A、B、C的弹力大小之比为3:3:1,当剪断C瞬间,小球的加速度大小及方向可能为( )
(2011?河南模拟)如图所示,小球质量为m,被三根质量不计的弹簧A、B、C拉住,弹簧间的夹角均为1200,小球平衡时,A、B、C的弹力大小之比为3:3:1,当剪断C瞬间,小球的加速度大小及方向可能为( )
