题目内容
A、B两物体分别以2v和v的初速度在同一水平面上滑行，已知两者与水平面间的动摩擦因数相同，且它们的质量关系是mA=4mB，则两者所能滑行的距离sA和sB之比与滑行的时间tA和tB之比应为（ ）A．sA：sB=1：4
B．sA：sB=4：1
C．tA：tB=1：2
D．tA：tB=2：1
【答案】分析：根据动能定理求解两者所能滑行的距离sA和sB之比．由动量定理求解滑行的时间tA和tB之比．
解答：解：根据动能定理得
对A：-μmAgsA=0-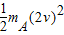
①
对B：-μmBgsB=0-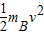
②
由①：②得sA：sB=4：1
根据动量定理得
对A：-μmAgtA=0-mA?2v③
对B：-μmBgtB=0-mBv ④
又mA=4mB，由③：④得到
tA：tB=2：1
故选BD
点评：本题涉及力在空间的效应可优先考虑运用动能定理，涉及力在时间的效应优先考虑动量定理，也可以根据牛顿第二定律和运动学公式结合求解．
解答：解：根据动能定理得
对A：-μmAgsA=0-
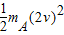①对B：-μmBgsB=0-
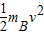②由①：②得sA：sB=4：1
根据动量定理得
对A：-μmAgtA=0-mA?2v③
对B：-μmBgtB=0-mBv ④
又mA=4mB，由③：④得到
tA：tB=2：1
故选BD
点评：本题涉及力在空间的效应可优先考虑运用动能定理，涉及力在时间的效应优先考虑动量定理，也可以根据牛顿第二定律和运动学公式结合求解．
练习册系列答案
星级口算天天练系列答案
相关题目
[物理-选修3-5]