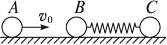题目内容
如图6-4-12所示,光滑轨道上,小车A、B用轻质弹簧连接,将弹簧压缩后用细绳系在A、B上,然后使A、B以速度v0沿轨道向右运动.运动中细绳突然断开,当弹簧第一次恢复到自然长度时,A的速度刚好为0,已知A、B的质量分别为mA、mB,且mA<mB.
求:
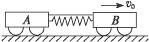
图6-4-12
(1)被压缩的弹簧具有的弹性势能Ep.
(2)试定量分析、讨论在以后的运动过程中,小车B有无速度为0的时刻.
求:

图6-4-12
(1)被压缩的弹簧具有的弹性势能Ep.
(2)试定量分析、讨论在以后的运动过程中,小车B有无速度为0的时刻.
(1) v02
v02
(2)小车B没有速度为零的时刻
 v02
v02(2)小车B没有速度为零的时刻
(1)设弹簧第一次恢复到自然长度时B的速度为vB,以A、B弹簧为系统动量守恒
(mA+mB)v0=mB·vB ①
机械能守恒
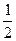 (mA+mB)v02+Ep=
(mA+mB)v02+Ep=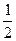 mB·vB2 ②
mB·vB2 ②
由①②解出
Ep= v02. ③
v02. ③
(2)设以后运动过程中B的速度为0时,A的速度为vA,此时弹簧的弹性势能为Ep′.由动量守恒得(mA+mB)v0=mA·vA ④
由机械能守恒有
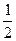 (mA+mB)v02+Ep=
(mA+mB)v02+Ep=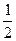 mAvA2+Ep′ ⑤
mAvA2+Ep′ ⑤
由④⑤有
Ep′=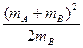 v02-
v02-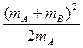 v02
v02
因mA<mB,所以Ep′<0
弹性势能小于0是不可能的,所以B的速度没有等于0的时刻.
(mA+mB)v0=mB·vB ①
机械能守恒
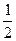 (mA+mB)v02+Ep=
(mA+mB)v02+Ep=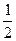 mB·vB2 ②
mB·vB2 ②由①②解出
Ep=
 v02. ③
v02. ③(2)设以后运动过程中B的速度为0时,A的速度为vA,此时弹簧的弹性势能为Ep′.由动量守恒得(mA+mB)v0=mA·vA ④
由机械能守恒有
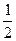 (mA+mB)v02+Ep=
(mA+mB)v02+Ep=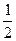 mAvA2+Ep′ ⑤
mAvA2+Ep′ ⑤由④⑤有
Ep′=
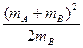 v02-
v02-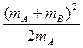 v02
v02因mA<mB,所以Ep′<0
弹性势能小于0是不可能的,所以B的速度没有等于0的时刻.

练习册系列答案
相关题目