题目内容
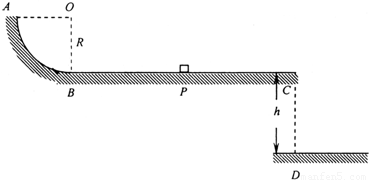
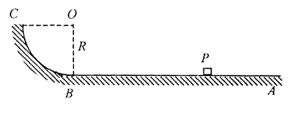
固定的轨道ABC如图，其中水平轨道AB与半径为R的1/4光滑圆弧轨道BC相连接，AB与圆弧相切于B点．质量为m的小物块静止在水平轨道上的P点，它与水平轨道间的动摩擦因数为
＝0.25，PB＝2R．用大小等于2mg的水平恒力推动小物块，当小物块运动到B点时，立即撤去推力．（小物块可视为质点．）
（1）求小物块沿圆弧轨道上升后，可能达到的最大高度H．
（2）如果水平轨道AB足够长，试确定小物块最终停在何处？
（1）3.5R （2）小物块最终停在B点右侧，距B点14R远处
解析:
（1）设：小物块在水平面上受到的水平恒力为F＝2mg，阻力为f，当质点运动到B点时速度为
．从P到B，根据动能定理，有：
①
②
N＝mg ③ （共4分）
三式联立，解得：
④ （2分）
质点从B到C，沿光滑曲面运动，机械能守恒，有：
⑤ （2分）
解得：
⑥ （2分）
质点从C点竖直上抛，达到的最大高度为h，
⑦ （2分）
所以小物块运动过程中离水平地面的最大高度为：
H＝R＋h＝3.5R （2分）
（2）由于机械能守恒，小物块从曲面上落回B点时的速度大小等于
，即：
⑧
小物块从B点向A方向运动，滑行至最远，有：
⑨
⑩ （三式共2分）
由④、⑧、⑨、⑩式联立，解得：
（2分）
代入数据：s＝14R
即：小物块最终停在B点右侧，距B点14R远处． （2分）
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
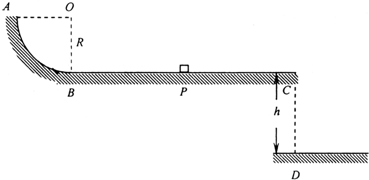
固定的轨道ABC如图所示，其中水平轨道AB与半径为R的1/4光滑圆弧轨道BC相连接，AB与圆弧相切于B点．质量为m的小物块静止在水平轨道上的P点，它与水平轨道间的动摩擦因数为μ=0.25，PB=2R．现用大小等于2mg的水平恒力推动小物块，当小物块运动到B点时，立即撤去推力．（小物块可视为质点．）
光滑圆弧轨道AB相连接，BC与圆弧相切于B点，水平轨道距离地面的高度为h．质量为m的小物块静止在水平轨道上的p点，PB=2R．用水平恒力推动小物块向左运动，当小物块运动到B点时，立即撤去推力，此后小物块沿光滑圆弧轨道运动并被向上抛出，小物块上升后，相对于水平轨道可以达到的最大高度为5R．小物块沿轨道返回后，在水平轨道上向右运动了BC=4R后，从C点飞出并落到水平地面上．（小物块可视为质点，忽略空气阻力）
R，可以测量出小物块从C点飞出后，落地点到D点的水平距离为3R．求：
