题目内容
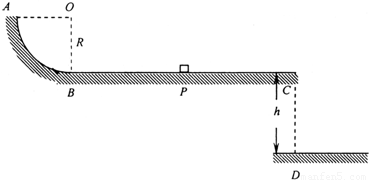
 固定的轨道ABC如图所示,其中水平轨道AB与半径为R的1/4光滑圆弧轨道BC相连接,AB与圆弧相切于B点.质量为m的小物块静止在水平轨道上的P点,它与水平轨道间的动摩擦因数为μ=0.25,PB=2R.现用大小等于2mg的水平恒力推动小物块,当小物块运动到B点时,立即撤去推力.(小物块可视为质点.)
固定的轨道ABC如图所示,其中水平轨道AB与半径为R的1/4光滑圆弧轨道BC相连接,AB与圆弧相切于B点.质量为m的小物块静止在水平轨道上的P点,它与水平轨道间的动摩擦因数为μ=0.25,PB=2R.现用大小等于2mg的水平恒力推动小物块,当小物块运动到B点时,立即撤去推力.(小物块可视为质点.)(1)求小物块沿圆弧轨道上升后,可能达到的最高点距AB面的高度H.
(2)如果水平轨道AB足够长,试确定小物块最终停在何处?
分析:(1)从A点运动到最高点的过程中,重力做负功,摩擦力做负功,可用动能定理列式求解;
(2)对从最高点到最后停止位置运用动能定理,可列式求解;也可对从A点开始到最后停止的全部过程运用动能定理列式求解.
(2)对从最高点到最后停止位置运用动能定理,可列式求解;也可对从A点开始到最后停止的全部过程运用动能定理列式求解.
解答:解:(1)小物块从A运动到最高点的全部过程中,推力做做正功,摩擦力做负功,重力做负功,由动能定理
F(2R)-μmg(2R)-mgH=0
又根据题意有 F=2mg
解得 H=3.5R
即可能达到的最高点距AB面的高度为3.5R.
(2)从最高点返回过程,重力做正功,摩擦力做负功,设物块最终停止在与B点相距x远处,则据动能定理
mgH-μmgx=0
解得 x=14R
即小物块最终停在B点右侧据B点14R处.
F(2R)-μmg(2R)-mgH=0
又根据题意有 F=2mg
解得 H=3.5R
即可能达到的最高点距AB面的高度为3.5R.
(2)从最高点返回过程,重力做正功,摩擦力做负功,设物块最终停止在与B点相距x远处,则据动能定理
mgH-μmgx=0
解得 x=14R
即小物块最终停在B点右侧据B点14R处.
点评:运用动能定理列式,要灵活选择运动过程,如果选择确当,通常可以使计算过程大为简化,因而能用动能定理的题,尽量用动能定理求解,同时要注意过程的选择,以简化为原则!

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
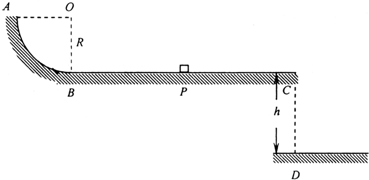
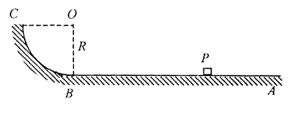
 光滑圆弧轨道AB相连接,BC与圆弧相切于B点,水平轨道距离地面的高度为h.质量为m的小物块静止在水平轨道上的p点,PB=2R.用水平恒力推动小物块向左运动,当小物块运动到B点时,立即撤去推力,此后小物块沿光滑圆弧轨道运动并被向上抛出,小物块上升后,相对于水平轨道可以达到的最大高度为5R.小物块沿轨道返回后,在水平轨道上向右运动了BC=4R后,从C点飞出并落到水平地面上.(小物块可视为质点,忽略空气阻力)
光滑圆弧轨道AB相连接,BC与圆弧相切于B点,水平轨道距离地面的高度为h.质量为m的小物块静止在水平轨道上的p点,PB=2R.用水平恒力推动小物块向左运动,当小物块运动到B点时,立即撤去推力,此后小物块沿光滑圆弧轨道运动并被向上抛出,小物块上升后,相对于水平轨道可以达到的最大高度为5R.小物块沿轨道返回后,在水平轨道上向右运动了BC=4R后,从C点飞出并落到水平地面上.(小物块可视为质点,忽略空气阻力) R,可以测量出小物块从C点飞出后,落地点到D点的水平距离为3R.求:
R,可以测量出小物块从C点飞出后,落地点到D点的水平距离为3R.求: