��Ŀ����
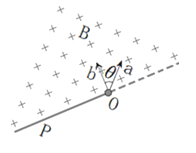
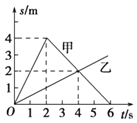
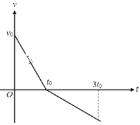
����Ŀ������m����飨����Ϊ�ʵ㣩��v0�ij��ٶȴ������=30���Ĵֲ�б���ϵ�P����б�������˶�������ߵ������ԭ·���ص�������P�㣬���ٶ���ʱ��仯��ͼ����ͼ��ʾ���Ҳ��ƿ�������������˵������ȷ���ǣ� ��
A. ������ܵ�������Ħ������С֮��Ϊ5��3
B. �������������˷�Ħ���������Ĺ���Ϊ![]()
C. ��������������������Ħ����������
D. ��������������������Ħ��������֮��10��1
���𰸡�BD
��������
����ϻ����»���λ�ƴ�С��ȣ�����λ��ʱ�乫ʽ�������ٶȹ�ϵ����ţ�ٵڶ��������������Ħ����֮�ȡ��ɶ��ܶ�������˷�Ħ�������Ĺ����������˷�Ħ���������Ĺ��ʡ�������������������Ϊ�㡣�ɳ����Ķ���������������Ħ��������֮�ȡ�
A�����鷵�ص�������P��ʱ�ٶȴ�СΪv����������ϻ����»���λ�ƴ�С��ȣ���
![]() ����ã�
����ã�![]()
��������ϻ��ļ��ٶ�Ϊ![]()
�»��ļ��ٶȴ�СΪ![]()
����ţ�ٵڶ�����
�ϻ��� mgsin��+f=ma1
�»��� mgsin��-f=ma2
�������![]() ����mg��f=10��3����A������
����mg��f=10��3����A������
B����������̣��ɶ��ܶ�����![]() ���ɽ�ã�
���ɽ�ã�![]() ��������������˷�Ħ���������Ĺ���Ϊ
��������������˷�Ħ���������Ĺ���Ϊ![]() ����B��ȷ��
����B��ȷ��
C������������������Ϊ�㣬��Ħ��������С����C������
D������������������ IG=mg3t0=3mgt0��Ħ�������� If=f2t0-ft0=0.3mgt0������ IG��If=10��1����D��ȷ��
��Ӧѡ��BD��