题目内容
【题目】如图所示,长为L的细绳的一端固定于O点,另一端系一个小球,在O点的正下方L/2钉一个光滑的钉子A,小球开始时θ=60°的位置摆下.则细绳碰到钉子前后,下列说法正确的是()
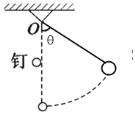
A. 绳对小球的拉力之比为2:3B. 小球所受合外力之比为1:2
C. 小球做圆周运动的线速度之比为2:3D. 小球做圆周运动的角速度之比为1:2
【答案】ABD
【解析】
A.在最低点由牛顿第二定律得Tmg=m![]() ,则拉力为T=mg+m
,则拉力为T=mg+m![]() ,和钉子接触前绳子拉力为T1=mg+m
,和钉子接触前绳子拉力为T1=mg+m![]() =2mg,接触钉子后半径变为原来的一半,绳子对小球的拉力T′=mg+m
=2mg,接触钉子后半径变为原来的一半,绳子对小球的拉力T′=mg+m![]() =3mg,所以接触钉子前后绳子的拉力之比为2:3,故A正确;
=3mg,所以接触钉子前后绳子的拉力之比为2:3,故A正确;
B.线速度大小不变,半径变为原来的一半,向心力(合力)增大为原来的2倍,故B正确;
C.小球由初始位置到最低点的过程中,由动能定理得:mgl(1-cos60°)=![]() mv2,则到达最低点的速度为
mv2,则到达最低点的速度为![]() ,和钉子接触瞬间速度不突变,故C错误;
,和钉子接触瞬间速度不突变,故C错误;
D.根据ω=![]() 知,线速度不变,半径变为原来的一半,故角速度变为原来的两倍,所以角速度之比为1:2,故D正确;
知,线速度不变,半径变为原来的一半,故角速度变为原来的两倍,所以角速度之比为1:2,故D正确;

练习册系列答案
相关题目