题目内容
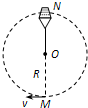 (2007?西城区模拟)如图所示的是杂技演员表演的“水流星”.一根细长绳的一端,系着一个盛了水的容器.以绳的另一端为圆心,使容器在竖直平面内做半径为R的圆周运动.N为圆周的最高点,M为圆周的最低点.若“水流星”通过最低点时的速度v=
(2007?西城区模拟)如图所示的是杂技演员表演的“水流星”.一根细长绳的一端,系着一个盛了水的容器.以绳的另一端为圆心,使容器在竖直平面内做半径为R的圆周运动.N为圆周的最高点,M为圆周的最低点.若“水流星”通过最低点时的速度v=| 5gR |
分析:根据动能定理求出“水流星”通过最高点的速度,根据牛顿第二定律去判断绳子对容器有无拉力,水对桶底部是否有压力.
解答:解:A、根据动能定理得,-mg?2R=
mv′2-
mv2,解得最高点的速度v′=
.故A错误.
B、对桶中的水分析,有N+mg=m
,解得N=0.知水对桶底压力恰好为零,水恰好不流出.故B错误,C正确.
D、对整体受力分析,有:F+mg=m
,解得F=0,绳子的拉力为零.故D错误.
故选C.
| 1 |
| 2 |
| 1 |
| 2 |
| gR |
B、对桶中的水分析,有N+mg=m
| v′2 |
| R |
D、对整体受力分析,有:F+mg=m
| v′2 |
| R |
故选C.
点评:解决本题的关键知道物体在竖直平面中做圆周运动,在最高点的临界情况,以及知道向心力的来源,运用牛顿第二定律进行求解.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 (2007?西城区一模)如图所示,在半径为R,质量分布均匀的某星球表面,有一倾角为θ的斜坡.以初速度v0向斜坡水平抛出一个小球.测得经过时间t,小球垂直落在斜坡上的C点.求:
(2007?西城区一模)如图所示,在半径为R,质量分布均匀的某星球表面,有一倾角为θ的斜坡.以初速度v0向斜坡水平抛出一个小球.测得经过时间t,小球垂直落在斜坡上的C点.求: (2007?西城区一模)根据α粒子散射实验,卢瑟福提出了原子的核式结构模型.下图表示了原子核式结构模型的α粒子散射图景.图中实线表示α粒子的运动轨迹.其中一个α粒子在从a运动到b、再运动到c的过程中(α粒子在b点时距原子核最近),下列判断正确的是( )
(2007?西城区一模)根据α粒子散射实验,卢瑟福提出了原子的核式结构模型.下图表示了原子核式结构模型的α粒子散射图景.图中实线表示α粒子的运动轨迹.其中一个α粒子在从a运动到b、再运动到c的过程中(α粒子在b点时距原子核最近),下列判断正确的是( )