题目内容
 如图所示,两根完全相同的光滑金属导轨POQ固定在水平桌面上,导轨间的夹角为θ,导轨单位长度的电阻为r.导轨所在空间有垂直于桌面向下的匀强磁场.t=0时刻将一电阻不计的金属杆MN,在外力作用下以恒定速度v从O点开始向右滑动.在滑动过程中保持MN垂直于两导轨间夹角的平分线,且与导轨接触良好,导轨和金属杆足够长.下列关于电路中电流大小I、金属杆MN间的电压U、外力F及电功率P与时间t的关系图象中正确的是( )
如图所示,两根完全相同的光滑金属导轨POQ固定在水平桌面上,导轨间的夹角为θ,导轨单位长度的电阻为r.导轨所在空间有垂直于桌面向下的匀强磁场.t=0时刻将一电阻不计的金属杆MN,在外力作用下以恒定速度v从O点开始向右滑动.在滑动过程中保持MN垂直于两导轨间夹角的平分线,且与导轨接触良好,导轨和金属杆足够长.下列关于电路中电流大小I、金属杆MN间的电压U、外力F及电功率P与时间t的关系图象中正确的是( )分析:(1)求出t时刻导体棒的有效切割长度,结合切割产生的感应电动势和闭合电路欧姆定律求出电流强度的大小.
(2)由欧姆定律得到U的表达式.
(3)当导体棒做匀速直线运动时,水平外力等于安培力,根据平衡求出水平拉力的表达式.
(3)导体棒内电流大小恒定,抓住R与时间成正比,得到功率表达式.
根据各量的表达式选择图象.
(2)由欧姆定律得到U的表达式.
(3)当导体棒做匀速直线运动时,水平外力等于安培力,根据平衡求出水平拉力的表达式.
(3)导体棒内电流大小恒定,抓住R与时间成正比,得到功率表达式.
根据各量的表达式选择图象.
解答:解:A、t时刻导体棒有效的切割长度为L=2vttan
=kt(k=2vtan
)
回路中感应电动势为E=BLv
总电阻为R=(2vt?tan
+2
)r
则感应电流I=
=
=
=定值,故A正确.
B、金属杆MN间的电压U=BLMNv-I(2vt?tan
)r,U随着时间均匀减小.故B错误.
C、导体棒做匀速直线运动,则有F=F安=BIL=BIkt∝t,故C错误.
D、电功率P=I2R=I2?(2vt?tan
+2
)r∝t.故D正确.
故选AD
| θ |
| 2 |
| θ |
| 2 |
回路中感应电动势为E=BLv
总电阻为R=(2vt?tan
| θ |
| 2 |
vttan
| ||
sin
|
则感应电流I=
| E |
| R |
Bv(2vt?tan
| ||||||||
(2vt?tan
|
| Bv | ||||
(1+
|
B、金属杆MN间的电压U=BLMNv-I(2vt?tan
| θ |
| 2 |
C、导体棒做匀速直线运动,则有F=F安=BIL=BIkt∝t,故C错误.
D、电功率P=I2R=I2?(2vt?tan
| θ |
| 2 |
vttan
| ||
sin
|
故选AD
点评:本题关键是根据法拉第电磁感应定律、欧姆定律、电阻定律得到感应电流不变,再得到其他各量的表达式,即可进行判断.

练习册系列答案
相关题目

 我国发射的“神州六号”载人宇宙飞船绕地球运动的周期约为90min.如果把它绕地球的运动看作是匀速圆周运动,该飞船的运动和在轨道上运行的地球同步卫星的运动相比较,该飞船的轨道半径
我国发射的“神州六号”载人宇宙飞船绕地球运动的周期约为90min.如果把它绕地球的运动看作是匀速圆周运动,该飞船的运动和在轨道上运行的地球同步卫星的运动相比较,该飞船的轨道半径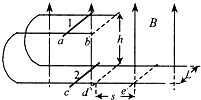 (2008?绵阳模拟)如图所示,在磁感应强度大小为B、方向竖直向上的匀强磁场中,有两根本身不相连接的光滑金属导轨处在竖直平面内,构成与水平面平行的上、下两层.在两水平导轨面上各放一根完全相同的质量为m的匀质金属杆1 和2,开始时两根金属杆都与轨道垂直,分别静止在a 处和c 处.两导轨面相距为h,导轨间宽为L,导轨足够长且电阻不计,每根金属杆电阻为r.现给金属杆1 一个水平向右的冲量使它具有初速度v0,金属杆1 离开右端b 时金属杆2 正好在b 的正下方d 处,金属杆1 落在下层导轨的e 处.d 与e 之间的距离为S.
(2008?绵阳模拟)如图所示,在磁感应强度大小为B、方向竖直向上的匀强磁场中,有两根本身不相连接的光滑金属导轨处在竖直平面内,构成与水平面平行的上、下两层.在两水平导轨面上各放一根完全相同的质量为m的匀质金属杆1 和2,开始时两根金属杆都与轨道垂直,分别静止在a 处和c 处.两导轨面相距为h,导轨间宽为L,导轨足够长且电阻不计,每根金属杆电阻为r.现给金属杆1 一个水平向右的冲量使它具有初速度v0,金属杆1 离开右端b 时金属杆2 正好在b 的正下方d 处,金属杆1 落在下层导轨的e 处.d 与e 之间的距离为S. 如图所示,光滑水平面上放置甲、乙两个内外壁都光滑的完全相同的气缸,气缸内各有一质量为m的活塞,密封完全相同的两部分气体(分子力可以忽略),甲、乙间用一根轻质水平细线相连接.现对甲气缸施一水平向左的恒定拉力F作用,甲气缸内气体的压强为p1,体积为V1;乙气缸内气体的压强为p2,体积为V2.设两部分气体始终和环境的温度相同,则( )
如图所示,光滑水平面上放置甲、乙两个内外壁都光滑的完全相同的气缸,气缸内各有一质量为m的活塞,密封完全相同的两部分气体(分子力可以忽略),甲、乙间用一根轻质水平细线相连接.现对甲气缸施一水平向左的恒定拉力F作用,甲气缸内气体的压强为p1,体积为V1;乙气缸内气体的压强为p2,体积为V2.设两部分气体始终和环境的温度相同,则( )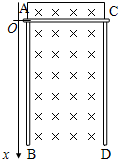 如图所示,AB和CD是两根特制的、完全相同的电阻丝导轨,固定在绝缘的竖直墙壁上,上端用电阻不计的导线相连接,两电阻丝导轨相距为L,一根质量为m、电阻不计的金属棒跨接在AC间,并处于x轴原点,与电阻丝导轨接触良好,且无摩擦,空间有垂直墙面向里的匀强磁场,磁感应强度为B.放开金属棒,它将加速下滑.
如图所示,AB和CD是两根特制的、完全相同的电阻丝导轨,固定在绝缘的竖直墙壁上,上端用电阻不计的导线相连接,两电阻丝导轨相距为L,一根质量为m、电阻不计的金属棒跨接在AC间,并处于x轴原点,与电阻丝导轨接触良好,且无摩擦,空间有垂直墙面向里的匀强磁场,磁感应强度为B.放开金属棒,它将加速下滑.