题目内容
18. 如图所示,固定于水平桌面上的光滑金属框架,处于竖直向上的匀强磁场中,导轨的宽度为L,金属棒ab搁在框架上,在恒力F作用下由静止开始运动.已知金属棒ab的电阻为r,电阻阻值为R,其余部分电阻不计,磁感应强度为B.求导体棒的最大速度.
如图所示,固定于水平桌面上的光滑金属框架,处于竖直向上的匀强磁场中,导轨的宽度为L,金属棒ab搁在框架上,在恒力F作用下由静止开始运动.已知金属棒ab的电阻为r,电阻阻值为R,其余部分电阻不计,磁感应强度为B.求导体棒的最大速度.
分析 导体棒先做加速度减小的变加速运动,当加速度为零时做匀速直线运动,速度达到最大,根据拉力F的功率等于电功率,列式求解.
解答 解:当导体棒匀速运动时速度最大,设最大速度为v.
则有:Fv=$\frac{{E}^{2}}{R+r}$
又 E=BLv
联立得:v=$\frac{F(R+r)}{{B}^{2}{L}^{2}}$
答:导体棒的最大速度为$\frac{F(R+r)}{{B}^{2}{L}^{2}}$.
点评 解决本题的关键要明确金属棒的运动过程,知道速度最大的条件:匀速运动,利用能量守恒列出功率关系求出,也可以由E=BLv、欧姆定律、安培力公式、平衡条件联立求解.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 声波与无线电波都是机械振动在介质中的传播 | |
| B. | 水面上的油膜在阳光照射下会呈现彩色,这是由于光的衍射造成的 | |
| C. | 狭义相对论认为时间与空间、物体的运动无关 | |
| D. | 真空中的光速在不同的惯性参考系中都是相同的,与光源和观察者的运动无关 |
2.2013年6月11日至26日.“神舟十号”飞船圆满完成了太空之行,期间还成功进行了人类历史上第二次太空授课,女航天员王亚平做了大量失重状态下的精美物理实验.关于失重状态,下列说法正确的是( )
| A. | 航天员仍受重力的作用 | B. | 航天员受力平衡 | ||
| C. | 航天员所受重力等于所需的向心力 | D. | 航天员不受重力的作用 |
13.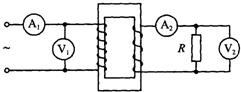 如图所示,理想变压器初级线圈匝数n1=1210匝,次级线圈匝数n2=121匝,初级电压u=311sin100πt V,次级负载电阻R=44Ω,不计电表对电路的影响,各电表的读书应为( )
如图所示,理想变压器初级线圈匝数n1=1210匝,次级线圈匝数n2=121匝,初级电压u=311sin100πt V,次级负载电阻R=44Ω,不计电表对电路的影响,各电表的读书应为( )
 如图所示,理想变压器初级线圈匝数n1=1210匝,次级线圈匝数n2=121匝,初级电压u=311sin100πt V,次级负载电阻R=44Ω,不计电表对电路的影响,各电表的读书应为( )
如图所示,理想变压器初级线圈匝数n1=1210匝,次级线圈匝数n2=121匝,初级电压u=311sin100πt V,次级负载电阻R=44Ω,不计电表对电路的影响,各电表的读书应为( )| A. |  读数为0.05A 读数为0.05A | B. |  读数为311V 读数为311V | C. |  读数为0.5A 读数为0.5A | D. |  读数为31.1V 读数为31.1V |
3.如图甲所示,理想变压器原、副线圈的匝数之比为10:1,b是原线圈的中心抽头,图中电表均为理想的交流电表,定值电阻R=10Ω,其余电阻均不计.从某时刻开始在原线圈c、d两端加上如图乙所示的交变电压.则下列说法中正确的有( )
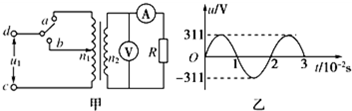

| A. | 当单刀双掷开关与a连接时,电压表的示数为22V | |
| B. | 当单刀双掷开关与a连接且在t=0.01s时,电流表示数为零 | |
| C. | 当单刀双掷开关由a拨向b时,原线圈的输入功率变大 | |
| D. | 当单刀双掷开关由a拨向b时,副线圈输出电压的频率仍为50Hz |
7.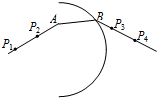 某同学在做测玻璃折射率的实验中,使用的是半圆形玻璃砖,P1、P2、P3、P4是按顺序插在软木板上的大头针,如图所示.下述实验操作中正确的是( )
某同学在做测玻璃折射率的实验中,使用的是半圆形玻璃砖,P1、P2、P3、P4是按顺序插在软木板上的大头针,如图所示.下述实验操作中正确的是( )
 某同学在做测玻璃折射率的实验中,使用的是半圆形玻璃砖,P1、P2、P3、P4是按顺序插在软木板上的大头针,如图所示.下述实验操作中正确的是( )
某同学在做测玻璃折射率的实验中,使用的是半圆形玻璃砖,P1、P2、P3、P4是按顺序插在软木板上的大头针,如图所示.下述实验操作中正确的是( )| A. | 若任意选取P1、P2连线的方向和入射点A的位置,都可以在圆弧外侧适当位置处插上第三个大头针同时挡住P1、P2的像 | |
| B. | 如果入射点A恰在玻璃砖圆心处,可不使用大头针P4 | |
| C. | 可以用P1、P2连线作为入射光线,也可以用P4、P3连线作为入射光线 | |
| D. | 为减小误差,P1、P2间距和P3、P4间距应适当大一些 | |
| E. | 本实验可以不做任何标记,撤掉玻璃砖后连接P1P2和P3P4计算折射率 |
8. 如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l,木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l,木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
 如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l,木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l,木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )| A. | 木块b比木块a先开始滑动 | |
| B. | 相对圆盘运动前,a、b所受的摩擦力始终相等 | |
| C. | ω=$\sqrt{\frac{2kg}{3l}}$是b开始滑动的临界角速度 | |
| D. | 当ω=$\sqrt{\frac{kg}{2l}}$时,a所受摩擦力的大小为$\frac{1}{2}$kmg |
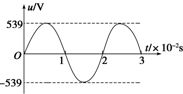 有一正弦交流电,它的电压随时间变化的图象如图所示,试写出:
有一正弦交流电,它的电压随时间变化的图象如图所示,试写出: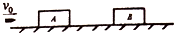 如图所示,光滑水平面上静止有质量均为2m的小滑块A、B,质量为m的子弹以水平向右的速度v0射入木块A,子弹穿出A后又水平射入木块B而未穿出,此后B与A之间的距离保持不变,求:
如图所示,光滑水平面上静止有质量均为2m的小滑块A、B,质量为m的子弹以水平向右的速度v0射入木块A,子弹穿出A后又水平射入木块B而未穿出,此后B与A之间的距离保持不变,求: