题目内容
14. 如图所示,内壁光滑的半球形容器固定在水平面上.将一劲度系数为k1的轻弹簧一端固定在半球形容器底部O′处(O为球心),弹簧另一端与质量为m的小球相连,小球静止于P点.此时容器所受的压力为F1,现把O′与球间的弹簧换成劲度系数为k2的轻弹簧,小球仍静止(球仍在容器内),此时容器所受的压力为F2,则F1与F2的大小关系为( )
如图所示,内壁光滑的半球形容器固定在水平面上.将一劲度系数为k1的轻弹簧一端固定在半球形容器底部O′处(O为球心),弹簧另一端与质量为m的小球相连,小球静止于P点.此时容器所受的压力为F1,现把O′与球间的弹簧换成劲度系数为k2的轻弹簧,小球仍静止(球仍在容器内),此时容器所受的压力为F2,则F1与F2的大小关系为( )| A. | F1=F2 | B. | F1>F2 | ||
| C. | F1<F2 | D. | 因k1、k2大小关系未知,故无法确定 |
分析 对小球进行受力分析可知,小球受重力、支持力及弹簧的弹力而处于静止,由共点力的平衡条件可求得小球受到的轻弹簧的弹力及小球受到的支持力,然后又牛顿第三定律说明即可.
解答 解:对小球进行受力分析如图所示,由图中几何关系可知,△OO′P∽△PBA
所以:$\frac{OP}{OO′}=\frac{PA}{PB}=\frac{G}{{F}_{N}}$
所以:FN=G
即小球受到的支持力始终等于小球的重力,与小球的位置无关,所以F1=F2;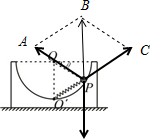
故选:A
点评 共点力平衡问题重点在于正确选择研究对象,本题运用隔离法进行受力分析得出结论.基础题目.

练习册系列答案
相关题目
4.物理学的发展离不开许多物理学家的智慧和奋斗,我们学习物理知识的同时也要学习他们的精神,记住他们的贡献.关于他们的贡献,以下说法正确的是( )
| A. | 爱因斯坦通过实验发现通电导线周围存在磁场,并提出了判断磁场方向的左手定则 | |
| B. | 奥斯特通过近十年的艰苦探索终于发现了“磁生电”的规律 | |
| C. | 法拉第通过实验发现了电磁感应现象,并总结出了感应电流方向的判断方法 | |
| D. | 变化的磁场能够在周围空间产生电场,是麦克斯韦最先提出的基本假设之一 |
5.汽车A在红绿灯前停住,绿灯亮起时起动,以0.4m/s2的加速度做匀加速运动,经过30s后以该时刻的速度做匀速直线运动.设在绿灯亮的同时,汽车B以8m/s的速度从A车旁边驶过,且一直以相同的速度做匀速直线运动,运动方向与A车相同,则从绿灯亮时开始( )
| A. | A车在加速过程中与B车相遇? | B. | A、B相遇时速度相同? | ||
| C. | 相遇时A车做匀速运动? | D. | 两车可能再次相遇? |
2.一弹簧振子振动过程中的某段时间内其加速度数值越来越大,则在这段时间内( )
| A. | 振子的速度越来越大 | |
| B. | 振子正在向平衡位置运动 | |
| C. | 振子的速度方向与加速度方向一定相同 | |
| D. | 以上说法都不正确 |
9.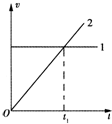 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )
 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )| A. | 图线2表示竖直分运动的v-t图线 | |
| B. | t1时刻的速度方向与初速度方向夹角为30° | |
| C. | t1时间内的竖直位移与水平位移之比为$\frac{1}{2}$ | |
| D. | 2t1时刻的速度方向与初速度方向夹角为60° |
3.在下列四个核反应方程中,符号“X”表示中子的是( )
| A. | ${\;}_{13}^{27}$Al+${\;}_{0}^{1}$n→${\;}_{12}^{27}$Mg+X | B. | ${\;}_{11}^{24}$Na→${\;}_{12}^{24}$Mg+X | ||
| C. | ${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+X | D. | ${\;}_{52}^{239}$U→${\;}_{93}^{239}$Np+X |
 如图所示,质量为0.4kg的木块以2m/s的速度水平地滑上静止的平板小车,车的质量为1.6kg,木块与小车之间的摩擦系数为0.2(g取10m/s2).设小车足够长,求:
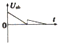
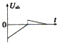
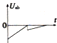
如图所示,质量为0.4kg的木块以2m/s的速度水平地滑上静止的平板小车,车的质量为1.6kg,木块与小车之间的摩擦系数为0.2(g取10m/s2).设小车足够长,求: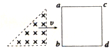 如图,有方向垂直于纸面向里的匀强磁场,磁场仅限于虚线边界所围的等腰直角三角形区域内,一固定的正方形金属框,其边长与三角形的直角边相同,每条边的材料及粗细均相同,现让有界匀强磁场向右匀速通过金属框,且金属框的下边与磁场区域的下边在同一直线上.在磁场通过金属框的过程中,从磁场边界到达ab边开始计时,能正确反映电势差Uab随时间变化的图象是( )
如图,有方向垂直于纸面向里的匀强磁场,磁场仅限于虚线边界所围的等腰直角三角形区域内,一固定的正方形金属框,其边长与三角形的直角边相同,每条边的材料及粗细均相同,现让有界匀强磁场向右匀速通过金属框,且金属框的下边与磁场区域的下边在同一直线上.在磁场通过金属框的过程中,从磁场边界到达ab边开始计时,能正确反映电势差Uab随时间变化的图象是( )