题目内容
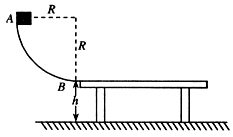
如图所示，固定光滑圆弧轨道AB，半径为R=0.8m，末端水平。水平面上质量为m1=2kg、高H=0.4m的方凳紧靠在圆弧AB的末端，方凳上表面与圆弧相切。现有一个质量为m2=2kg的滑块（视为质点）从A端由静止沿圆弧下滑，在B点滑上方凳，经过一段时间后从方凳右端滑落。已知：方凳与地面、滑块与凳面间的动摩擦因数分别为μ1=0.2、μ2=0.5；方凳从开始运动到停止运动，在水平面上运动的位移x=27cm。（取g=10m/s2）求：
（1）滑块滑上方凳时的速度；
（2）滑块与方凳分离时，方凳的速度；
（3）滑块刚落地时，滑块与方凳右端之间的距离（结果保留三位有效数字）。
（1）滑块滑上方凳时的速度；
（2）滑块与方凳分离时，方凳的速度；
（3）滑块刚落地时，滑块与方凳右端之间的距离（结果保留三位有效数字）。
解：（1）滑块从A滑到B的过程，机械能守恒，设滑块滑到B的速度v0
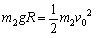
解得：v0 =4m/s
（2）方凳由静止开始做匀加速直线运动，直至滑块从其右端滑落，设此段位移为x11；然后做匀减速直线运动直至停止，设此段位移为x12，中间最大速度为v1
依据动能定理：μ2m2g x11-μ1（m1+ m2）g x11＝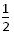
m1v12
-μ1m1g x12＝－
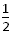m1v12
x11+ x12＝x
解得：v1=0.6m/s，x11＝0.18m，x12＝0.09m
（3） 设滑块在凳面运动的时间为t1，滑块从其右端滑落时的速度为v2
对方凳：v1=a1t1
μ2m2g -μ1（m1+ m2）g ＝m1a1
对滑块：v0-v2=a2t1
μ2m2g ＝m2a2
解得：v2=1m/s
滑块从凳面滑落后做平抛运动，设时间为t2，水平位移为x2
则有：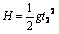
，
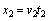
滑块落地后木块继续滑行（0.3－t2）s，设位移为x13，加速度为a3
a3=μ1g，x13＝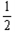
a3（0.3－t2）2
木凳不能撞到物块，则滑块与方桌右端之间的距离 x ＝x2+ x13- x12＝0.193m
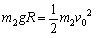
解得：v0 =4m/s
（2）方凳由静止开始做匀加速直线运动，直至滑块从其右端滑落，设此段位移为x11；然后做匀减速直线运动直至停止，设此段位移为x12，中间最大速度为v1
依据动能定理：μ2m2g x11-μ1（m1+ m2）g x11＝
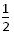m1v12 -μ1m1g x12＝－
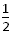m1v12 x11+ x12＝x
解得：v1=0.6m/s，x11＝0.18m，x12＝0.09m
（3） 设滑块在凳面运动的时间为t1，滑块从其右端滑落时的速度为v2
对方凳：v1=a1t1
μ2m2g -μ1（m1+ m2）g ＝m1a1
对滑块：v0-v2=a2t1
μ2m2g ＝m2a2
解得：v2=1m/s
滑块从凳面滑落后做平抛运动，设时间为t2，水平位移为x2
则有：
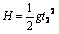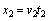
，滑块落地后木块继续滑行（0.3－t2）s，设位移为x13，加速度为a3
a3=μ1g，x13＝
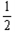a3（0.3－t2）2木凳不能撞到物块，则滑块与方桌右端之间的距离 x ＝x2+ x13- x12＝0.193m
练习册系列答案
教学练新同步练习系列答案
相关题目
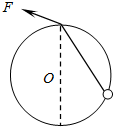（2010?松江区二模）如图所示，固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔．质量为m的小球套在圆环上．一根细线的下端系着小球，上端穿过小孔用手拉住．现拉动细线，使小球沿圆环缓慢上移．在移动过程中手对线的拉力F和轨道对小球的弹力N的大小变化情况是（ ）
如图所示，在光滑的水平面上停放一上表面水平的平板车C，C质量为3m，在车上左端放有质量为2m木块B，车左端靠于固定在竖直平面内半径为R的
