题目内容
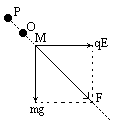
如图所示,一光滑圆环固定于一水平向右的匀强电场中,在最低点有一个初速度为v0,质量为m,带电量为+q的小球,且qE=mg,试求:①为使小球能做圆周运动而不脱离圆环,圆环的半径R最多多大?
②小球在运动过程中的最大速率.

答案:
解析:
提示:
解析:
|
小球在电场中的受力如图其合力方向与水平面成
F= 而由能量守恒有 将①代入②得:R= 当小球达M点时速度最大,由能量关系有 所以vm= |
提示:
|
考虑重力与电场力的合力,分析其合成场(重力场与电场的合成),找出小球对应的“等效最高点”与”等效最低点”,然后利用做圆运动的特点及能量(机械能与电势能)守恒则可求解. |

练习册系列答案
相关题目