题目内容
如图所示，真空中存在竖直向上的匀强电场和水平向里的匀强磁场，一质量为m，带电荷量为q的质点恰能以速度v在竖直平面内做半径为R的匀速圆周运动，取t=0时质点在轨迹最低点，且重力势能为零，电势能也为零，则质点______时针（填“顺”或“逆”）转动，质点机械能的变化量随时间变化的关系式为△E=______．
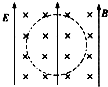
重力与电场力平衡，故电场力向上，由于电场方向向上，故电荷带正电；由于磁场方向是垂直向内，根据左手定则可知，转动方向逆时针；
洛伦兹力不做功，只有重力和电场力做功，故作用机械能和电势能相互转化，总量守恒，在最低点时，有：E=
mv2；
则重力势能的表达式为：Ep=mg（R-Rcosθ）=mgR（1-cosωt）=mgR（1-cos
t），
因动能不变，且重力势能为零，则机械能的变化量随时间变化的关系式为：△E=mgR（1-cos
t），
故答案为：逆，mgR（1-cos
t）．
洛伦兹力不做功，只有重力和电场力做功，故作用机械能和电势能相互转化，总量守恒，在最低点时，有：E=
| 1 |
| 2 |
则重力势能的表达式为：Ep=mg（R-Rcosθ）=mgR（1-cosωt）=mgR（1-cos
| v |
| R |
因动能不变，且重力势能为零，则机械能的变化量随时间变化的关系式为：△E=mgR（1-cos
| v |
| R |
故答案为：逆，mgR（1-cos
| v |
| R |
练习册系列答案
名校课堂系列答案
相关题目
，宽为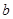
，两板间的距离为
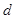，将管道沿风海流方向固定在风海流中，在金属板之间加一水平匀强磁场，磁感应强度大小为
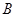，方向由南向北，用导线将M、N外侧连接电阻为
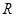的航标灯（图中未画出）。工作时，海水从东向西流过管道，在两金属板之间形成电势差，可以对航标灯供电，设管道内海水的流速处处相同，且速率恒为
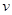，海水的电阻率为
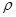，海水所受摩擦力与流速成正比，比例系数为
。
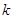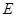的大小，并判断M、N两板哪个板电势较高；
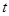时间内磁流体发电机消耗的总机械能。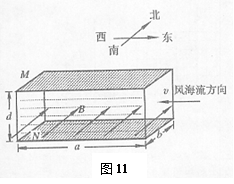
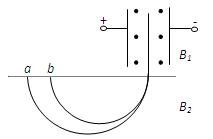
cm的圆形区域内，有一个水平方向的匀强磁场，磁感应强度大小为B2=0.1T，方向垂直纸面向外。M、N为竖直平行放置的相距很近的两金属板， S1、S2为M、N板上的两个小孔，且S1、S2跟O点在垂直极板的同一水平直线上。金属板M、N与一圆形金属线圈相连，线圈的匝数n=1000匝，面积S=0.2m2，线圈内存在着垂直纸面向外的匀强磁场，磁感应强度大小随时间变化的规律为B1=B0+kt（T），其中B0、k为常数。另有一水平放置的足够长的荧光屏D，O点跟荧光屏D之间的距离为H=2R。比荷为2×105 C/kg的正离子流由S1进入金属板M、N之间后，通过S2向磁场中心射去，通过磁场后落到荧光屏D上。离子的初速度、重力、空气阻力及离子之间的作用力均可忽略不计。问：
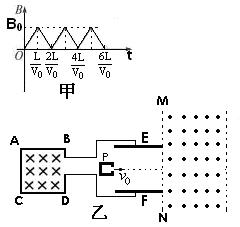
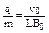的正离子， 离子从两板间飞出后进入如图所示的匀强磁场区域，MN为磁场的左边界，磁场的磁感强度为B0，已知t=0时刻和t=
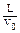两时刻恰好有两个离子从P中以初速度v0沿EF的中央轴线射入两板间，不计离子受到的重力。
