题目内容
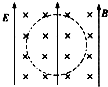
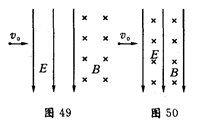
如图所示ABCD为边长为L的单匝正方形金属线框处在垂直于线框平面的匀强磁场中，磁场的磁感强度随时间变化的规律如图甲所示，E、F为平行正对的两金属板，板长和板间距均为L，两金属板通过导线分别与金属线框的端点相连，P为一粒子源，能够发射速度为v0比荷为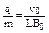
的正离子， 离子从两板间飞出后进入如图所示的匀强磁场区域，MN为磁场的左边界，磁场的磁感强度为B0，已知t=0时刻和t=
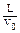两时刻恰好有两个离子从P中以初速度v0沿EF的中央轴线射入两板间，不计离子受到的重力。
（1）试判断两离子能否从两板间穿出进入MN右侧的磁场区域。
（2）求离子进入磁场时的速度与v0的夹角。
（3）如果两粒子均能从磁场的左边界MN飞离磁场，求两离子在磁场中运动的时间之比。
（4）为了保证两离子均再从磁场的左边界MN飞离，求磁场区域的最小宽度。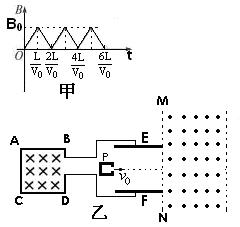
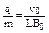的正离子， 离子从两板间飞出后进入如图所示的匀强磁场区域，MN为磁场的左边界，磁场的磁感强度为B0，已知t=0时刻和t=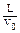两时刻恰好有两个离子从P中以初速度v0沿EF的中央轴线射入两板间，不计离子受到的重力。（1）试判断两离子能否从两板间穿出进入MN右侧的磁场区域。
（2）求离子进入磁场时的速度与v0的夹角。
（3）如果两粒子均能从磁场的左边界MN飞离磁场，求两离子在磁场中运动的时间之比。
（4）为了保证两离子均再从磁场的左边界MN飞离，求磁场区域的最小宽度。
（1）由法拉第电磁感应定律：
…………………………①
由图得：
………………②
带电粒子进入电场后做匀加速曲线运动，由牛顿第二定律得：
…………………………… ③
偏转位移
……………………④
由题意设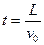
时可以出电场，此时
即粒子刚好从极板边界出电场进入磁场
（2）此时竖直方向速度
………………………………… ⑤
带入数据得
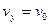
…………………………………⑥
进入磁场时速度与磁场的夹角为
（或如图由几何关系得：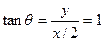
）
（3）两粒子进入磁场做圆周运动，轨迹如图
在磁场中运动时间为：
…………………………………………………⑦
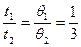
（4）由牛顿第二定律得：
…………………………………………⑧
…………………………………………………⑨
解得
为了保证两离子均再从磁场的左边界MN飞离，由几何关系的
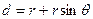…………………………………………………………⑩
得：
…………………………①由图得：
………………②带电粒子进入电场后做匀加速曲线运动，由牛顿第二定律得：
…………………………… ③偏转位移
……………………④由题意设
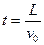时可以出电场，此时即粒子刚好从极板边界出电场进入磁场
（2）此时竖直方向速度
………………………………… ⑤带入数据得
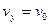
…………………………………⑥进入磁场时速度与磁场的夹角为
（或如图由几何关系得：
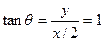）（3）两粒子进入磁场做圆周运动，轨迹如图
在磁场中运动时间为：
…………………………………………………⑦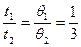（4）由牛顿第二定律得：
…………………………………………⑧ …………………………………………………⑨ 解得
为了保证两离子均再从磁场的左边界MN飞离，由几何关系的
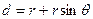…………………………………………………………⑩得：
略
练习册系列答案
相关题目
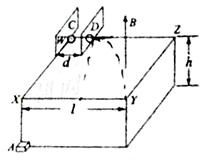
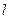=1.8m，距地面h=0.8m。平行板电容器的极板CD间距d=0.1m且垂直放置于台面，C板位于边界WX上，D板与边界WZ相交处有一小孔。电容器外的台面区域内有磁感应强度B=1T、方向竖直向上的匀强磁场。电荷量q=5×10-13C的微粒静止于W处，在CD间
加上恒定电压U=2.5V，板间微粒经电场加速后由D板所开小孔进入磁场（微粒始终不与极板接触），然后由XY边界离开台面。在微粒离开台面瞬时，静止于X正下方水平地面上A点的滑块获得一水平速度，在微粒落地时恰好与之相遇。假定微粒在真空中运动、极板间电场视为匀强电场，滑块视为质点，滑块与地面间的动摩擦因数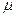
=0.2，取g=10m/s2