题目内容
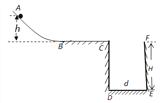
【题目】如图所示，在某竖直平面内，光滑曲面AB与水平面BC平滑连接于B点，BC右端连接一口深为H，宽度为d的深井CDEF，一个质量为m的小球放在曲面AB上，可从距BC面不同的高度处静止释放小球，已知ＢＣ段长L,小球与BC间的动摩擦因数为μ，取重力加速度g=10m/s2．则：
（1）若小球恰好落在井底E点处，求小球释放点距BC面的高度h1；
（2）若小球不能落在井底，求小球打在井壁EF上的最小动能Ekmin和此时的释放点距BC面的高度h2。
【答案】（1）
（2）
【解析】（1）小球由A到C，由动能定理得
①
自C点水平飞出后，由平抛运动规律得
②
③
由①②③得
④
若小球恰好落在井底E处，则
代入④式得小球的释放点距BC面的高度为
（2）若小球不能落在井底，设打在EF上的动能为
，则x=d
由②③式得
小球由C到打在EF上，由动能定理得
代入
得： 
当
时， 
最小，且
此时小球的释放点距BC面的高度为
练习册系列答案
相关题目
