Question

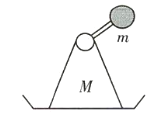
【题目】如图所示,木板倾角为37°时,质量为1kg的滑块m2恰能在木板上静止．木板的下端有一固定挡板，其上固定一个弹性势能为3J的锁定弹簧该弹簧的压缩量Δx=0.01m．弹簧上端放有与滑块m2完全相同的滑块m1(与弹簧不拴接),m1与m2相距d=1m．现解除弹簧锁定,在弹簧恢复原长时m1离开弹簧,与此同时,让m2以t=m/s的速度沿木板向下运动并最终与m1相碰,碰后两者粘在一起. (已知sin37°=0.6，cos37°=0.8，g=10m/s2， =2.4)．求:

(1)m1离开弹簧时的速度大小;

(2)m1、m2两者的碰撞位置距m2的初始位置多远;

(3)m1、m2的粘合体离开弹簧后最终静止在木板上的位置．

Answer 1

【答案】(1) 2.4m/s (2) 0.75m (3) 0.125m

【解析】

（1）由题可知

，

解得：

μ=0.75

离开弹簧时，弹簧处于原长状态，故该过程中，

对m1：

解得

（2）对弹簧弹开后的m1：

减速至停止历时：

该过程经历位移：

s1==0.24m

而对该过程中的m2：

判断：

∵

故m1、m2碰前m1已停止

即碰撞位置距m2的初始端为：

（3）由动量守恒可得

解得：

m1、m2碰撞后，粘合体将沿斜面向下匀速运动压缩弹簧，将联合整体的动能全部转化为弹簧的弹性势能

因为：

故弹簧被压缩至最短时的形变量仍为，故弹簧被压缩至最短后至粘合体静止的过程中，

解得：

即：粘合体在最后静止在距m1初位置0.125m处。