题目内容
一辆自行车以10m/s的速度从某站出发开始向前行驶,经过30s后,有一辆摩托车以同向50m/s,加速度大小为2m/s2做减速运动通过该站,问在经过多长时间两车可到达空间同一点?
【答案】分析:抓住位移相等,根据位移时间公式求出两车到达空间同一点的时间,注意摩托车减速速度为零后不再运动.
解答:解:设经过t时间两车到达空间同一点,则:

代入数据得:10(t+30)=50t-t2
解得:t1=10s,t2=30s.
摩托车刹车到停止所需的时间: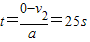 .故t2=30s舍去.
.故t2=30s舍去.
当t=25s时,自行车距离车站的距离:x1=v1(t+30)=550m
摩托车距离车站的距离: .
.
摩托车停止后,自行车追上摩托车还需的时间:t′= .
.
则:t=25+7.5s=32.5s.
答:在经过10s或32.5s两车可到达空间同一点.
点评:解决本题的关键抓位移关系,通过匀变速直线运动的位移公式进行求解,注意该问题是刹车问题,摩托车减速到零后不再运动.
解答:解:设经过t时间两车到达空间同一点,则:

代入数据得:10(t+30)=50t-t2
解得:t1=10s,t2=30s.
摩托车刹车到停止所需的时间:
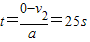 .故t2=30s舍去.
.故t2=30s舍去.当t=25s时,自行车距离车站的距离:x1=v1(t+30)=550m
摩托车距离车站的距离:
 .
.摩托车停止后,自行车追上摩托车还需的时间:t′=
 .
.则:t=25+7.5s=32.5s.
答:在经过10s或32.5s两车可到达空间同一点.
点评:解决本题的关键抓位移关系,通过匀变速直线运动的位移公式进行求解,注意该问题是刹车问题,摩托车减速到零后不再运动.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目