题目内容
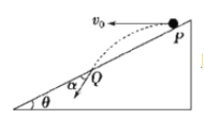
【题目】如图所示,一长度L=7m的传送带与水平方向间的夹角α=30°,在电动机带动下以v=4m/s的速率顺时针匀速转动。在传送带上端接有一个斜面,斜面表面与传送带表面都在同一平面内。将质量m=2kg可视作质点的物体无初速地放在传送带底端,物体经传送带作用后能到达斜面顶端且速度为零。若物体与传送带及物体与斜面间的动摩擦因数都为![]() ,g=10m/s2,且最大静摩擦力等于滑动摩擦力,求:
,g=10m/s2,且最大静摩擦力等于滑动摩擦力,求:
(1)物体在从传送带底端运动到斜面顶端过程中传送带对物体所做的功;
(2)传送带上方所接的斜面长度。
【答案】(1)84J (2)0.64m
【解析】
物体先在传送带上做初速度为零的匀加速直线运动,先根据牛顿第二定律求出物体的加速度,再由速度公式求出物体在传送带相对滑动的时间,此过程中物体通过的位移大于传送带的长度,所以物体一直做匀速直线运动,根据动能定理求解传送带对物体所做的功;物体离开传送带后做匀减速运动,到斜面顶端时速度为零,根据牛顿第二定律和运动学公式结合求解传送带上方所接的斜面长度;
解:(1)对物体,先在传送带上做初速度为零的匀加速直线运动,根据牛顿第二定律得:![]()
又![]()
解得:![]() ,沿斜面向上
,沿斜面向上
设物体速度经过时间t与传送带相等,则由:![]()
解得:![]()
此过程中物体通过的位移为![]()
所以物体一直做匀速直线运动,则有![]()
离开传送带时速度为:![]()
对整个过程,由动能定理:![]()
得传送带对物体所做的功:![]()
(2)物体到斜面上以后,根据牛顿第二定律得:![]()
解得:![]()
由![]() 解得传送带上方所接的斜面长度:
解得传送带上方所接的斜面长度:![]()

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目