题目内容
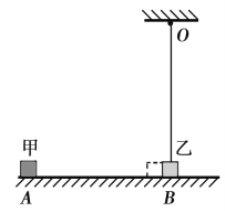
【题目】如图所示,可视为质点的物块甲、乙分别处于同一水平面上的A、B两点,在B点的正上方O处用一根不可伸长的轻绳将物块乙悬挂,使乙对水平面的压力恰好为零。物块甲以初速度![]() 沿直线由A向B运动,在B点与甲发生碰撞(碰撞时间极短) ,碰撞后甲、乙粘在一起向右摆动,上升达到的最高位置与O点等高。已知
沿直线由A向B运动,在B点与甲发生碰撞(碰撞时间极短) ,碰撞后甲、乙粘在一起向右摆动,上升达到的最高位置与O点等高。已知![]() =5m/s,甲与水平面间的动摩擦因数μ=0.2,A、B两点间的距离L=2.25m,甲、乙的质量关系为
=5m/s,甲与水平面间的动摩擦因数μ=0.2,A、B两点间的距离L=2.25m,甲、乙的质量关系为![]() ,重力加速度
,重力加速度![]()
(1)物块甲由A运动到B的时间;
(2)碰撞前瞬间物块甲的速度大小;
(3)轻绳的长度。
【答案】(1) t=0.5s;(2) v1 =4m/s;(3 ) l=0.45m
【解析】
(1)碰撞前物块甲在水平面上做匀减速直线运动,设甲的运动时间、加速度大小和碰撞前瞬间速度大小分别为t、a和![]() ,由牛顿运动定律和匀减速直线运动规律可知
,由牛顿运动定律和匀减速直线运动规律可知
![]()
![]()
联立解得t=0.5s
(2) 根据匀变速规律可知,![]() ,可得v1 =4m/s。
,可得v1 =4m/s。
(3)设物块甲、乙碰撞后瞬间的速度大小为v2、细绳长为l,根据动量守恒和机械能守恒得
![]()
![]()
联立解得l=0.45m 。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目