题目内容
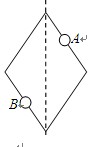
在直径1.6m的圆柱体一端截出一圆锥，如下图所示，在看到剖面上，三角形的三边之比为3:4:5, 圆柱体可绕其中心对称轴匀速旋转。将一小木块放置在斜面的中点，它与斜面间动摩擦力因素为0.25，若小木块保持在此位置不动，则圆柱体旋转的角速度应为多大.（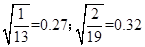
；g取10m/s2）
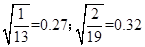；g取10m/s2）3.2rad/s≤ω≤5.4rad/s
试题分析：当圆柱体旋转角速度最小为ωmin时，木块有沿斜面向下滑动趋势，木块受最大静摩擦力f的方向沿斜面向上。木块受重力mg、斜面支持力N和静摩擦f,如图所示。木块在水平面内作匀速圆周运动，向心加速度
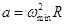，R=0.4m。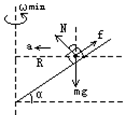
根据牛顿第二定律得
水平方向：
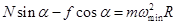①竖直方向： Ncosα+fsinα=mg ②
又 f=μN ③
联立①、②、③解得
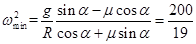
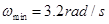
当圆柱体旋转角速度最大为
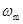时，木块有沿斜面向上滑动趋势，木块受最大静摩擦力f的方向沿斜面向下。木块还受重力mg和斜面支持力N′作用，如图所示。木块加速度
。
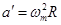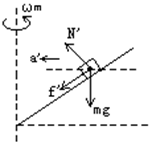
由牛顿第二定律得
水平方向：
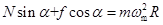④竖直方向： Ncosα-fsinα=mg ⑤
又 f′=μN′ ⑥
联立④、⑤、⑥解得
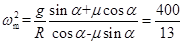
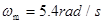
圆柱体旋转的角速度ω应为3.2rad/s≤ω≤5.4rad/s
点评：关键是知道当圆柱体旋转角速度最大木块有沿斜面向上滑动趋势，木块受最大静摩擦力f的方向沿斜面向下。当圆柱体旋转角速度最小木块有沿斜面向下滑动趋势，木块受最大静摩擦力f的方向沿斜面向上。
练习册系列答案
相关题目
。 
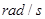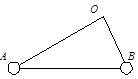
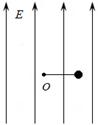
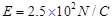、方向竖直向上的匀强电场，在电场内一长为L=0.5m的绝缘细线一端固定于O点，另一端拴着质量m=0.5kg、电荷量
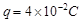的小球。现将细线拉至水平位置，将小球由静止释放，当小球运动到最高点时细线受到的拉力恰好达到它能承受的最大值而断裂，取
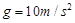。求：