��Ŀ����
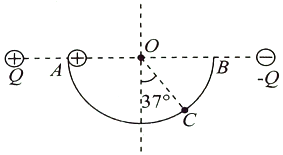
����Ŀ����ͼ��ʾ�����������ֵ����ͬһˮƽ���ϣ��������ߵ��е�ΪO����ֱ���ڵİ�Բ���⻬��Ե�����ֱ��ABˮƽ��Բ����O�㣬Բ���İ뾶ΪR��CΪԲ���ϵ�һ�㣬OCΪ��ֱ����ļн�Ϊ37�㣬һ�����Ϊ+q������Ϊm�Ĵ���С��ӹ����A���ɾ�ֹ�ͷţ��ع����������͵�ʱ���ٶ�v=2![]() ��gΪ�������ٶȣ�ȡ����Զ������Ϊ�㣬������˵����ȷ���ǣ�������
��gΪ�������ٶȣ�ȡ����Զ������Ϊ�㣬������˵����ȷ���ǣ�������
A. �糡��A��ĵ���Ϊ![]()
B. �糡��B��ĵ���Ϊ![]()
C. С���˶���B��ʱ�Ķ���Ϊ2mgR
D. С���˶���C��ʱ���䶯��������ܵĺ�Ϊ1.6mgR
���𰸡�AC
��������ȡ����Զ������Ϊ0������͵㴦����Ϊ0��С���A���˶�����͵�����У��ɶ��ܶ����ɵã�mgR+qUAO��![]() mv2����� UAO��
mv2����� UAO��![]() ����UAO=��A-0������A��
����UAO=��A-0����ã���A��![]() ����A��ȷ���ɶԳ��Կ�֪��UAO=UBO����Ϊ����A-0=0-��B�����У���B��
����A��ȷ���ɶԳ��Կ�֪��UAO=UBO����Ϊ����A-0=0-��B�����У���B��![]() ����B����С���A���˶���B������У��ɶ��ܶ����ã�Ek=qUAB=2mgR����C��ȷ��С������͵㴦�Ķ��ܺ͵����ܵ��ܺ�Ϊ��E1��
����B����С���A���˶���B������У��ɶ��ܶ����ã�Ek=qUAB=2mgR����C��ȷ��С������͵㴦�Ķ��ܺ͵����ܵ��ܺ�Ϊ��E1��![]() mv2+0��2mgR������͵��˶���C����̣����ܡ������ܡ��������ܵ������غ㣬����������������Ϊ����Ep=mgR��1-cos37����=0.2mgR
mv2+0��2mgR������͵��˶���C����̣����ܡ������ܡ��������ܵ������غ㣬����������������Ϊ����Ep=mgR��1-cos37����=0.2mgR
�ʶ��ܡ������ܵ��ۺϼ�����0.2mgR������С����C��Ķ��ܺ͵����ܵ��ܺ�Ϊ��E2=E1-0.2mgR=1.8mgR����D����ѡAC.

 �Ķ��쳵ϵ�д�
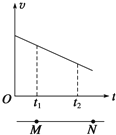
�Ķ��쳵ϵ�д�����Ŀ����1��ʵ���ҳ��õĵ��ʽ����ʱ���õ��ǵ�ѹ������Դ�����Ƶ��Ϊ50HZ��ij��ʵ����������һϵ�е��ֽ������ͼ���ɴ˿����жϣ����ֽ�����˶�����________�����������������ȱ�������ֱ���˶���ֽ����AB���˶���ʱ��t =____s��AB�ε�ƽ���ٶ�![]() ______m/s��������������λ��Ч���֣�
______m/s��������������λ��Ч���֣�

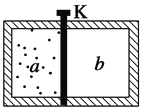
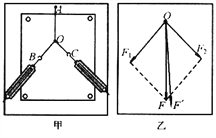
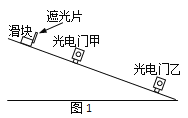
��2������ͼ1��ʾ��װ�ÿɲ���������б�����˶��ļ��ٶȡ�һб���ϰ�װ����������ţ����й�����ҹ̶���б���Ͽ����˴�������ż�λ�ÿ��ƶ�����һ�����ڹ�Ƭ�Ļ�����б���ϻ���ʱ������������Ŷ������ļ�ʱ��������ʾ���ڹ�Ƭ�ӹ���ż��������õ�ʱ��t���ı����ż�λ�ý��ж�β�����ÿ�ζ�ʹ�����ͬһ���ɾ�ֹ��ʼ�»��������׳߲����ס���֮��ľ���s��������Ӧ��tֵ�������������±���ʾ��
s(m) | 0.500 | 0.600 | 0.700 | 0.800 | 0.900 | 0.950 |
t(ms) | 292.9 | 371.5 | 452.3 | 552.8 | 673.8 | 776.4 |
s/t(m/s) | 1.71 | 1.62 | 1.55 | 1.45 | 1.34 | 1.22 |
���������պ���ͼ��
����֪������б���»�ʱ���ȼ����˶���������ٶȵĴ�Сa�����龭���������ʱ��˲ʱ�ٶ�v1������ֵs��t�ĸ�������֮��������Ĺ�ϵʽ��_________________��
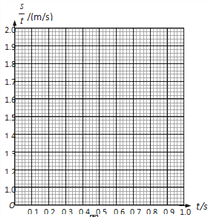
�ڸ��ݱ��и��������ݣ���ͼ2����������ֽ�ϻ���s/t-tͼ��_____________��
������������s/t-tͼ�ߣ��ó�������ٶȵĴ�С Ϊa=_______m/s2������2λ��Ч���֣���