题目内容
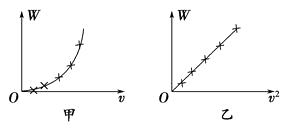
【题目】(2015·上海）两靠得较近的天体组成的系统成为双星，它们以两者连线上某点为圆心做匀速圆周运动，因而不至于由于引力作用而吸引在一起。设两天体的质量分布为m1和m2 ， 则它们的轨道半径之比Rm1: Rm2 ；速度之比Vm1: Vm2 。
【答案】m2：m1；m2：m1
【解析】双星角速度相同。向心力由万有引力提供，大小也相等，所以有: G
=m1
Rm1=m2Rm2, 所以Rm1: Rm2=m2：m1。 角速度一定，线速度与半径成正比，所以速度之比Vm1: Vm2=Rm1: Rm2=m2：m1
【考点精析】利用万有引力定律及其应用对题目进行判断即可得到答案，需要熟知应用万有引力定律分析天体的运动：把天体的运动看成是匀速圆周运动，其所需向心力由万有引力提供.即 F引=F向；应用时可根据实际情况选用适当的公式进行分析或计算.②天体质量M、密度ρ的估算．
练习册系列答案
相关题目
