题目内容
1．
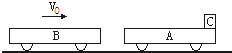如图所示．在光滑的水平地面上停着一辆质量为m1=20Kg的小车A，有一质量为m2=15Kg的小木块C静止于小车A的右端，另有一辆质量为m3=25Kg的小车B以V0=3m/s的速度向右运动，与小车A发生碰撞，碰撞后连在一起运动（两车相碰时间极短）．假定车A足够长，木块与小车A的动摩擦因数为?=0.2（g取10m/s2，计算结果小数点后保留两位）．试求：（1）碰撞结束瞬间小车A的速度大小
（2）木块在小车A上滑动的距离．
分析 （1）两车碰撞时系统的动量守恒，碰后两球的速度相等，根据动量守恒定律可求得A的速度；
（2）将两车及物体视为一个系统，由动量守恒定律可求得碰后的速度；再由功能关系可求得物体在小车上滑行的距离．
解答 解：A、B两车碰撞瞬间，设向右为正，由动量守恒定律得
m3V0=（m1+m3）V
解得V=1.67 m/s
②A、B两车以及木块为对象，由动量守恒定律得
m3V0=（m1+m3+m2）V共
由功能关系得
?m2gS=$\frac{1}{2}$（m1+m3）V2-$\frac{1}{2}$（m1+m3+m2）V共2
联立解得S=0.52 m
答：（1）碰撞结束瞬间小车A的速度大小为1.67m/s
（2）木块在小车A上滑动的距离为0.52m
点评 本题考查动量守恒定律的应用，要注意正确分析研究对象，明确是哪一个系统动量守恒，再注意明确正方向求解．
练习册系列答案
相关题目
12．在居室装修中经常用到花岗岩、大理石等装饰材料，据报道这些岩石都具有不同程度的放射性，放射出的α、β、γ射线，会导致细胞发生癌变及呼吸道等方面的疾病．根据有关放射性知识可知，下列说法正确的是（ ）
| A． | 氡的半衰期为3.8天，若取4个氡原子核，经7.6天后就一定剩下一个氡原子核了 | |
| B． | γ射线一般伴随着α或β射线产生，在这三种射线中，γ射线的穿透能力最强，电离能力最弱 | |
| C． | β衰变所释放的电子是原子核内的中子转变为质子时所产生的 | |
| D． | 若使放射性物质的温度升高，其半衰期将减小 | |
| E． | 铀核（${\;}_{92}^{238}$U）衰变为铅核（${\;}_{82}^{206}$Pb）的过程中，要经过8次α衰变和6次β衰变 |
如图所示，玻璃管的横截面S=1cm2，在玻璃管内有一段质量为m=0.1Kg的水银柱和一定量的理想气体，当玻璃管平放时气体柱的长度为l0=10cm，现把玻璃管正立，稳定后再将玻璃管倒立，经过较长时间后，水银柱再次稳定，求玻璃管由正立至倒立状态，水银柱相对于管底移动的距离，假设环境温度保持不变，大气压强取P0=1×105Pa，g=10m/s2．
16．
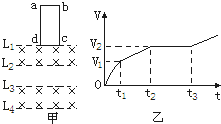如图甲所示．在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4，在L1和L2之间、L3和L4之间存在匀强磁场，磁感应强度大小均为1T，方向垂直于虚线所在平面，磁场宽度为L，现有一宽度cd=L=0.5m、质量为0.1kg、电阻为2Ω的矩形线圈abcd，将其从图示位置由静止释放（cd边与L1重合），速度随时间变化关系如图乙所示，t1时刻cd边与L2重合，t2时刻ab边与L3重合，t3时刻ab边与L4重合，已知t1～t2的时间间隔为0.6s，整个运动过程线圈平面始终处于竖直方向．（重力加速度g取10m/S2）则（ ）
如图甲所示．在竖直方向上有四条间距相等的水平虚线L1、L2、L3、L4，在L1和L2之间、L3和L4之间存在匀强磁场，磁感应强度大小均为1T，方向垂直于虚线所在平面，磁场宽度为L，现有一宽度cd=L=0.5m、质量为0.1kg、电阻为2Ω的矩形线圈abcd，将其从图示位置由静止释放（cd边与L1重合），速度随时间变化关系如图乙所示，t1时刻cd边与L2重合，t2时刻ab边与L3重合，t3时刻ab边与L4重合，已知t1～t2的时间间隔为0.6s，整个运动过程线圈平面始终处于竖直方向．（重力加速度g取10m/S2）则（ ）| A． | 在0～t1时间内，通过线圈的电荷量为0.25C | |
| B． | 线圈匀速运动的速度大小为8m/s | |
| C． | 线圈的长度为1m | |
| D． | 在0～t3时间内，线圈上产生的热量为4.2J |
6．
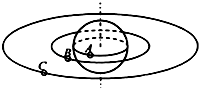中国航天局秘书长田玉龙2015年3月6日证实，将在2015年年底发射高分四号卫星，这是中国首颗地球同步轨道高时间分辨率对地观测卫星．如图所示，A是静止在赤道上随地球自转的物体；B、C是同在赤道平面内的两颗人造卫星，B位于离地高度等于地球半径的圆形轨道上，C是高分四号卫星．则下列关系正确的是（ ）
中国航天局秘书长田玉龙2015年3月6日证实，将在2015年年底发射高分四号卫星，这是中国首颗地球同步轨道高时间分辨率对地观测卫星．如图所示，A是静止在赤道上随地球自转的物体；B、C是同在赤道平面内的两颗人造卫星，B位于离地高度等于地球半径的圆形轨道上，C是高分四号卫星．则下列关系正确的是（ ）| A． | 物体A随地球自转的角速度大于卫星B的角速度 | |
| B． | 卫星B的线速度大于卫星C的线速度 | |
| C． | 物体A随地球自转的加速度大于卫星C的加速度 | |
| D． | 物体A随地球自转的周期大于卫星C的周期 |
13．
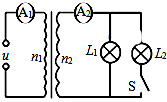如图所示，理想变压器的输入端接交流电压，输出端并联两只相同的小灯泡L1、L2，灯泡的额定电压为20V，额定功率为10W，电路连接了两只理想电流表A1、A2，导线电阻不计．开始时电键S断开，小灯泡L1恰好正常发光．下列说法正确的是（ ）
如图所示，理想变压器的输入端接交流电压，输出端并联两只相同的小灯泡L1、L2，灯泡的额定电压为20V，额定功率为10W，电路连接了两只理想电流表A1、A2，导线电阻不计．开始时电键S断开，小灯泡L1恰好正常发光．下列说法正确的是（ ）| A． | 原副线圈的匝数比为n1：n2=3$\sqrt{2}$：1 | |
| B． | 流过小灯泡L1的电流方向每秒改变10次 | |
| C． | 电键S闭合后，小灯泡L1变暗 | |
| D． | 电键S闭合后，电流表A1的读数变大 |
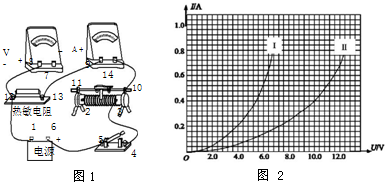
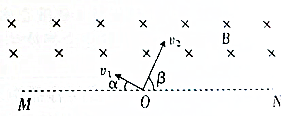如图所示，垂直纸面的平面MN将空间分成两部分，上方有垂直纸面向里的匀强磁场，磁感应强度为B，下方有匀强电场，大小方向未知，从MN上的O点，先后有两个带电粒子垂直磁场方向射入上方空间，其中甲粒子带负电，速度方向与MN的夹角α=30°，大小v1=v0，乙粒子带正电，速度方向与MN的夹角β=60°，大小v2=$\sqrt{3}$v0，两粒子质量皆为m、电荷量皆为q，且同时到达磁场边界的A、B两点（图中未画出），不计两粒子的重力及粒子间的相互作用．