��Ŀ����
11��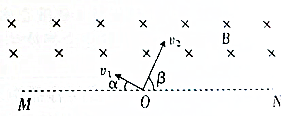 ��ͼ��ʾ����ֱֽ���ƽ��MN���ռ�ֳ������֣��Ϸ��д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB���·�����ǿ�糡����С����δ֪����MN�ϵ�O�㣬�Ⱥ��������������Ӵ�ֱ�ų����������Ϸ��ռ䣬���м����Ӵ����磬�ٶȷ�����MN�ļнǦ�=30�㣬��Сv1=v0�������Ӵ����磬�ٶȷ�����MN�ļнǦ�=60�㣬��Сv2=$\sqrt{3}$v0��������������Ϊm���������Ϊq����ͬʱ����ų��߽��A��B���㣨ͼ��δ�����������������ӵ����������Ӽ������ã�
��ͼ��ʾ����ֱֽ���ƽ��MN���ռ�ֳ������֣��Ϸ��д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB���·�����ǿ�糡����С����δ֪����MN�ϵ�O�㣬�Ⱥ��������������Ӵ�ֱ�ų����������Ϸ��ռ䣬���м����Ӵ����磬�ٶȷ�����MN�ļнǦ�=30�㣬��Сv1=v0�������Ӵ����磬�ٶȷ�����MN�ļнǦ�=60�㣬��Сv2=$\sqrt{3}$v0��������������Ϊm���������Ϊq����ͬʱ����ų��߽��A��B���㣨ͼ��δ�����������������ӵ����������Ӽ������ã���1�����������ڴų��߽��ϵĴ�����A��B֮��ľ���d��
��2���������ӽ���ų���ʱ������t��
��3����MN�·�����ǿ�糡ƽ����ֽ�棬���������ڵ糡�����������м�������ֱ���˶�����糡ǿ��E�Ĵ�С�ͷ���
���� ��1�����������ڴų���������Բ���˶��������������ṩ�����������������������˶��İ뾶��Ȼ���ϼ��ι�ϵ�������AB֮��ľ��룻
��2���������ת����Բ�Ľǣ�Ȼ����������ڴų��е��˶�ʱ�䣻
��3����ϼ���ֱ���˶�������A��B������������˶������Ȼ����ţ�ٵڶ��������˶�ѧ�Ĺ�ʽ���������
��� �⣺��1�����������ڴų���������Բ���˶��Ĺ켣��ͼ�������������ṩ�������ã�$qvB=\frac{m{v}^{2}}{r}$
���ԣ�${r}_{1}=\frac{m{v}_{1}}{qB}=\frac{m{v}_{0}}{qB}$
${r}_{2}=\frac{m{v}_{2}}{qB}=\frac{\sqrt{3}m{v}_{0}}{qB}$
��ͼ�м��ι�ϵ��֪��$AO={r}_{1}=\frac{m{v}_{0}}{qB}$��$OB=2��{r}_{2}cos��=2��\frac{\sqrt{3}m{v}_{0}}{qB}•\frac{\sqrt{3}}{2}=\frac{3m{v}_{0}}{qB}$
���ԣ�$d=AO+OB=\frac{4m{v}_{0}}{qB}$
��2����ͼ��֪��������ת���ĽǶ��ǣ���1=360��-2��=360-2��30=300�㣬
������ת���ĽǶȣ���2=360��-2��=36-2��60=240��
�����˶������ڣ�$T=\frac{2��r}{v}=\frac{2��m}{qB}$
�����˶���ʱ�������ڵĹ�ϵ��$\frac{��}{2��}=\frac{t}{T}$
���������ڴų����˶���ʱ�䣺${t}_{��}=\frac{300}{360}��T=\frac{5��m}{3qB}$��${t}_{��}=\frac{240}{360}��T=\frac{4��m}{3qB}$
�����ӽ���ų���ʱ������t=${t}_{��}-{t}_{��}=\frac{5��m}{3qB}-\frac{4��m}{3qB}=\frac{��m}{3qB}$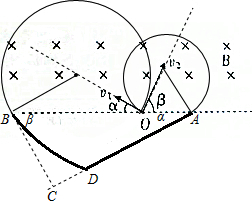
��3�����ڼ������ڵ糡����ֱ���˶������Ե糡���ķ����ؼ����ӵ��ٶȵķ��������Է��أ����Ե糡ǿ�ȵķ��������Ϸ����������˶��ķ����෴������߿��ܲ���������
���ڦ�=30�㣬��=60�㣬�ɴ��������ڴų����˶��ĶԳ��Կ�֪�����ӴӴų��������һ���ķ�����MN֮��ļн���Ȼ�ֱ��Ǧ��ͦ£��������ӴӴų���������ٶȵķ������ֱ����֪�������ٶȵķ�����BC��AC���糡���ķ�����AC�ķ���������BC��ֱ���������Ӽ����ȼ���ֱ���˶���������������ƽ���˶����������ӵ������͵��������ȣ����Լ��ٶ�Ҳ��ȣ���糡ǿ�ȵĴ�СΪE�����ٶȣ�$a=\frac{qE}{m}$
�������D������������ʱ�ڵ糡���˶���ʱ��Ϊt������BC�ķ��������ҵ��˶���$\overline{BC}={v}_{2}t$�����У�$\overline{BC}=d•sin��=d•sin30��=\frac{2m{v}_{0}}{qB}$
��λ�ƣ�$\overline{AD}={v}_{1}t+\frac{1}{2}a{t}^{2}$
�ҵ�λ�ƣ�$\overline{CD}=\frac{1}{2}a{t}^{2}$
$\overline{AD}+\overline{CD}=\overline{AC}=d•cos��=d��cos30��=2\sqrt{3}•\frac{m{v}_{0}}{qB}$
�������Ϸ��̣���ã�E=B•v0
�𣺣�1���������ڴų��߽��ϵĴ�����A��B֮��ľ�����$\frac{4m{v}_{0}}{qB}$��
��2�������ӽ���ų���ʱ������$\frac{��m}{3qB}$��
��3����MN�·�����ǿ�糡ƽ����ֽ�棬���������ڵ糡�����������м�������ֱ���˶����糡ǿ��E�Ĵ�СΪB•v0�����������ϣ���MN֮��ļн���30�㣮
���� ���⿼�����������ڴų��е��˶�ʱ�䣬��������ǿ�ų���������Բ���˶����������ת����Բ�Ľǡ��������ӵ����ڹ�ʽ����������ӵ��˶�ʱ�䣮

 С�����ϵ�д�
С�����ϵ�д�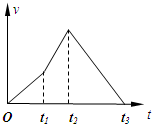 ij�Ƽ���ȤС����ʵ��װ��ģ�����������ǣ������ȼ��ӵ�����ֱ���գ�ȼ��ȼ�������ĵ�һ���ڶ���������䣬ʵ���в��������ֱ������ٶ�-ʱ��ͼ����ͼ��ʾ�����˶��в��ƿ���������ȼ��ȼ��ʱ������������С�㶨�������ж���ȷ���ǣ�������
ij�Ƽ���ȤС����ʵ��װ��ģ�����������ǣ������ȼ��ӵ�����ֱ���գ�ȼ��ȼ�������ĵ�һ���ڶ���������䣬ʵ���в��������ֱ������ٶ�-ʱ��ͼ����ͼ��ʾ�����˶��в��ƿ���������ȼ��ȼ��ʱ������������С�㶨�������ж���ȷ���ǣ�������| A�� | t2ʱ�����ǵ�����ߵ㣬t3ʱ��������ص��� | |
| B�� | ������0��t1ʱ���ڵļ��ٶȴ���t1��t2ʱ���ڵļ��ٶ� | |
| C�� | t1��t2ʱ�������Ǵ��ڳ���״̬��t2��t3ʱ�������Ǵ���ʧ��״̬ | |
| D�� | ������t2��t3ʱ���ڵļ��ٶȴ�С�����������ٶ� |
| A�� | ����糡��������治��ֱ����ô�糡ǿ�Ⱦ���һ�����ŵ�����ķ������ڵ��������ƶ���ɾ�������Ҫ�����������õ��������ǹ��ɷ� | |
| B�� | ����Ϊ���ʹ���������ˡ��������ڲ�������һ�ֻ��ε���-���ӵ������Ĺ۵� | |
| C�� | �ñ�ֵ�����������ٶ�����������������ʽΪa=$\frac{F}{m}$ | |
| D�� | ţ�����á���-�ؼ��顱������������������ |
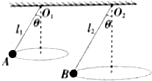 ��ͼ��ʾ��������ͬ��С��A��B�ó��ȷֱ�Ϊl1��l2��ϸ�ߣ�l1��l2���������컨���O1��O2�㣬������ˮƽ����������Բ���˶�������ϸ������ֱ��нǾ�Ϊ�ȣ���A��B��������ٶȷֱ�ΪvA��vB�����ٶȷֱ�Ϊ��A����B���ٶȷֱ�ΪaA��aB������ϸ�ߵ������ֱ�ΪFA��FB��������
��ͼ��ʾ��������ͬ��С��A��B�ó��ȷֱ�Ϊl1��l2��ϸ�ߣ�l1��l2���������컨���O1��O2�㣬������ˮƽ����������Բ���˶�������ϸ������ֱ��нǾ�Ϊ�ȣ���A��B��������ٶȷֱ�ΪvA��vB�����ٶȷֱ�Ϊ��A����B���ٶȷֱ�ΪaA��aB������ϸ�ߵ������ֱ�ΪFA��FB��������| A�� | vA��vB | B�� | ��A����B | C�� | aA=aB | D�� | FA��FB |
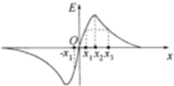 �ռ���һ��x��ԳƷֲ��ĵ糡���糡ǿ�Ⱦ���x�����ҹ涨��x������Ϊ������糡ǿ��E��x��仯��ͼ����ͼ��ʾ��ͼ�������ԭ��O�㣬����˵������ȷ���ǣ�������
�ռ���һ��x��ԳƷֲ��ĵ糡���糡ǿ�Ⱦ���x�����ҹ涨��x������Ϊ������糡ǿ��E��x��仯��ͼ����ͼ��ʾ��ͼ�������ԭ��O�㣬����˵������ȷ���ǣ�������| A�� | x1��x3����ĵ������ | |
| B�� | ��x���ϳ�ǿ���ĵ�������������һ������x2 | |
| C�� | ����ԭ��O��ĵ������ | |
| D�� | x1��-x1����ĵ������ |
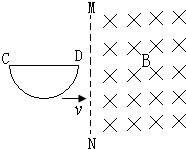 ��ͼ��ʾ��һ������ɰ뾶Ϊa�İ�Բ�αպϻ�·������MN�Ҳ��дŸ�Ӧǿ��ΪB����ǿ�ų�������ֱ�ڻ�·���ڵ�ƽ�棬��·���ٶ�v�������ٽ���ų���ֱ��CDʼ����MN��ֱ����D�㵽��߽翪ʼ��C�����ų�Ϊֹ�����н��۴�����ǣ�������
��ͼ��ʾ��һ������ɰ뾶Ϊa�İ�Բ�αպϻ�·������MN�Ҳ��дŸ�Ӧǿ��ΪB����ǿ�ų�������ֱ�ڻ�·���ڵ�ƽ�棬��·���ٶ�v�������ٽ���ų���ֱ��CDʼ����MN��ֱ����D�㵽��߽翪ʼ��C�����ų�Ϊֹ�����н��۴�����ǣ�������| A�� | CD��ֱ����ʼ�ղ��ܰ����� | B�� | ��Ӧ�綯�����ֵEm=Bav | ||
| C�� | ��Ӧ�������� | D�� | ��Ӧ�綯��ƽ��ֵ$\overline{E}$=$\frac{1}{4}$��Bav |
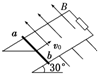 һ����Ϊm������Ϊr�Ľ�����ab����һ���ij��ٶ�v0��һ�⻬ƽ�н�����������ϻ��У�����ƽ����ˮƽ���30��ǣ��������϶���һ����R��������ͼ��ʾ���ų���ֱб�����ϣ�����ĵ��費�ƣ����������ϻ��е�ijһ�߶�֮���ַ��ص���ʱ���ٶȴ�СΪv����������ڻ��й����У�������
һ����Ϊm������Ϊr�Ľ�����ab����һ���ij��ٶ�v0��һ�⻬ƽ�н�����������ϻ��У�����ƽ����ˮƽ���30��ǣ��������϶���һ����R��������ͼ��ʾ���ų���ֱб�����ϣ�����ĵ��費�ƣ����������ϻ��е�ijһ�߶�֮���ַ��ص���ʱ���ٶȴ�СΪv����������ڻ��й����У�������| A�� | ���ϻ��е�ʱ��С�����»��е�ʱ�� | |
| B�� | �����ϻ���ʱ����R�ϲ����������������»���ʱ����R�ϲ��������� | |
| C�� | ���ϻ���ʱ�����»���ʱͨ������R�ĵ������� | |
| D�� | �����˴ӿ�ʼ�ϻ������س����㣬����R�ϲ���������Ϊ$\frac{1}{2}$m��v02-v2�� |
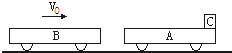 ��ͼ��ʾ���ڹ⻬��ˮƽ������ͣ��һ������Ϊm1=20Kg��С��A����һ����Ϊm2=15Kg��Сľ��C��ֹ��С��A���Ҷˣ�����һ������Ϊm3=25Kg��С��B��V0=3m/s���ٶ������˶�����С��A������ײ����ײ������һ���˶�����������ʱ�伫�̣����ٶ���A�㹻����ľ����С��A�Ķ�Ħ������Ϊ?=0.2��gȡ10m/s2��������С���������λ��������
��ͼ��ʾ���ڹ⻬��ˮƽ������ͣ��һ������Ϊm1=20Kg��С��A����һ����Ϊm2=15Kg��Сľ��C��ֹ��С��A���Ҷˣ�����һ������Ϊm3=25Kg��С��B��V0=3m/s���ٶ������˶�����С��A������ײ����ײ������һ���˶�����������ʱ�伫�̣����ٶ���A�㹻����ľ����С��A�Ķ�Ħ������Ϊ?=0.2��gȡ10m/s2��������С���������λ��������