题目内容
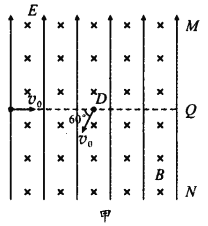
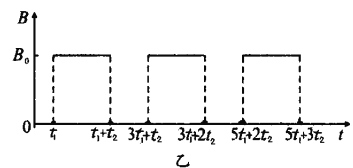
【题目】如图甲，竖直面MN的左侧空间中存在竖直向上的匀强电场（上、下及左侧无边界）。一个质量为m，电荷量为q，可视为质点的带正电的小球，以水平初速度
沿PQ向右做直线运动，若小球刚经过D点时（0此时开始计时t=0），在电场所在空间叠加如图乙所示随时间周期性变化，垂直纸面向里的匀强磁场，使得小球再次通过D点时速度方向如图所示与PQ连线成60°角，且以后能多次经过D点作周期性运动。图中
、
均为未知量，且
均小于小球在磁场中做圆周运动的周期。已知D、Q间的距离为L，忽略磁场变化造成的影响，重力加速度为g，求：
（1）电场强度E的大小；
（2）
的比值；
（3）当小球做周期性运动的周期最大时，求出此时的磁感应强度
及运动的最大周期
的大小。
【答案】（1）
（2）
（3）
； 
【解析】（1）未加磁场时，小球做匀速运动，由受力平衡得
（2）加上磁场后小球的运动情况如图所示：
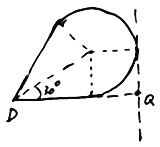
在
时间内，小球做匀速运动
，
在
时间内，小球做圆周运动，则
， 
，
解得
（3）由几何关系知;
，
洛伦兹力提供的向心力
在此段时间内走过的总位移为
，
由运动学公式得：
综上所述本题答案是：（1）
（2）
（3）
； 
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
