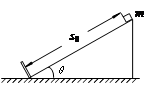
题目内容
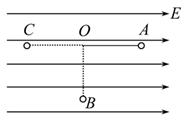
如图所示的“S”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,放置在竖直平面内,轨道弯曲部分是由两个半径相等的半圆对接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,轨道在水平面上不可移动。弹射装置将一个小球(可视为质点)从a点水平弹射向b点并进入轨道,经过轨道后从最高点d水平抛出。已知小球与地面ab段间的动摩擦因数μ=0.2,不计其它机械能损失,ab段长L=1.25m,圆的半径R=0.1m,小球质量m=0.01kg,轨道质量为M=0.26kg,g=10m/s2,求: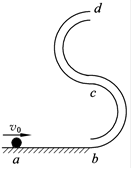
(1)要使小球从d点抛出后不碰轨道,小球的初速度v0需满足什么条件?
(2)设小球进入轨道之前,轨道对地面的压力大小等于轨道自身的重力,当v0至少为多少时,小球经过两半圆的对接处c点时,轨道对地面的压力为零。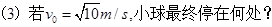
(1) 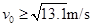 (2) 6 m/s (3)a点
(2) 6 m/s (3)a点
解析试题分析:
(1)设小球到达d点时速度为vd,由动能定理得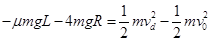 (1)
(1)
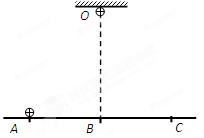
如小球由d点做平抛运动刚好经过图中的O点,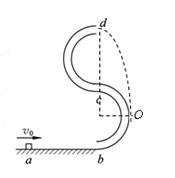
则有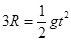 (2)
(2) 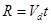 (3)
(3)
联立(1)(2)(3)并代入数据解得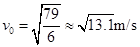 (4) 即初速度满足
(4) 即初速度满足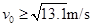 (5)
(5)
(2)设小球到达c点处速度为vc,由动能定理,得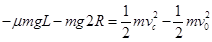 (6)
(6)
当小球通过c点时,由牛顿第二定律得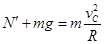 (7)
(7)
要使轨道对地面的压力为零,则有
N′=Mg (8)
联立⑥⑦⑧并代入数值,解得小球的最小速度
v0="6" m/s (9)
(3)小球能通过d点,需满足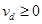 ,由动能定理
,由动能定理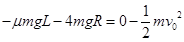 (10)
(10)
得: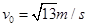
 小球过不了d点而沿轨道原路返回 (11)
小球过不了d点而沿轨道原路返回 (11)
对整个过程由动能定理,有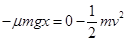 (12)
(12)
得 x=2.5m (13) 即小球最终停在a处 (14)
考点:竖直平面的圆周运动往往结合能否完成圆周运动的临界条件以及平抛运动进行考查,解题思路是正确受力分析列向心力方程,然后结合功能关系求解.

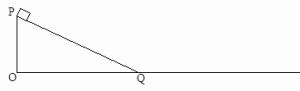
 ,sin370=0.6,cos370=0.8。
,sin370=0.6,cos370=0.8。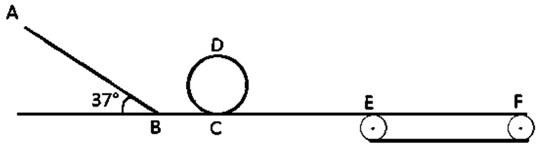
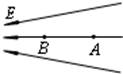
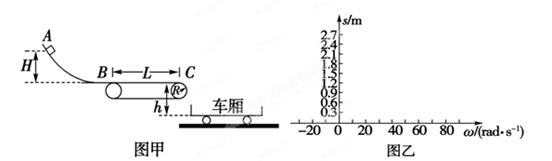
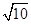 m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求
m/s的水平初速度向B滑行,滑过s = 1m的距离,与B相碰,碰撞时间极短,碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求