题目内容
【题目】一辆汽车在十字路口等候绿灯，当绿灯亮时汽车以
的加速度开始加速行驶，恰在这时一辆自行车以
的速度匀速驶来，从后边超过汽车。则汽车从路口启动后，在追上自行车之前经过多长时间两车相距最远？此时两车的距离是多少？经过多长时间汽车追上自行车？
【答案】2s，6m，4s.
【解析】试题分析：在相遇前相距最远的临界条件是两车速度相等，根据速度时间关系求得此过程中时间，再根据位移时间关系求得相距最远的距离；根据位移相等求得汽车追上自行车的时间。
两车相距最远时速度相等，即有：v汽=v自
根据速度时间关系可得： 
汽车运动时间为： 
此过程中的自地车位移：x自=v自t=6×2m=12m
此过程中汽车的位移为： 
所以汽车追上前两车相距最远距离为：△xmax=x自-x汽=12-6m=6m
汽车追上自行车时两车位移相等，则有： 
进一步可得： 
带入数据解得： 
练习册系列答案
相关题目
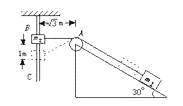
【题目】如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在C点．每隔0.2秒钟通过速度传感器测量物体的瞬时速度，表给出了部分测量数据．（重力加速度g=10m/s2）求：
t（s） | 0.0 | 0.2 | 0.4 | … | 1.2 | 1.4 | 1.6 | … |
v（m/s） | 0.0 | 1.0 | 2.0 | … | 1.1 | 0.7 | 0.3 | … |
（1）斜面的倾角α；
（2）物体与水平面之间的动摩擦因数μ；
（3）t=0.6s时的瞬时速度v．
