��Ŀ����
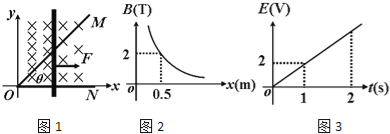
����Ŀ����ͼ1��ʾ��ˮƽ���ڵ�ֱ������ϵ�ĵ�һ�����дų��ֲ�������ֱ��ˮƽ�����£��Ÿ�Ӧǿ����y�᷽��û�б仯���������x�Ĺ�ϵ��ͼ2��ʾ��ͼ����˫���ߣ��������ǽ����ߣ���������=45���Ĺ⻬���������� MON�̶���ˮƽ���ڣ�ON��x���غϣ�һ����ON��ֱ�ij��������ˮƽ���ҵ������������ص���MON���һ�����������ڻ���������ʼ�ձ����뵼�����ýӴ�����֪t=0ʱ�������λ�ڶ���O���������������Ϊm=2kg��OM��ON�Ӵ���O��ĽӴ�����ΪR=0.5����������費�ƣ���·�綯��E��ʱ��t�Ĺ�ϵ��ͼ3��ʾ��ͼ���ǹ�ԭ���ֱ�ߣ���
��1��t=2sʱ����������ĵ���ǿ��I2�Ĵ�С��
��2��1��2sʱ���ڻ�·�������ĵ���q�Ĵ�С��
��3�����������������ˮƽ����F����λ��N���������x����λ��m���Ĺ�ϵʽ��
���𰸡���1��t=2sʱ����������ĵ���ǿ��I2�Ĵ�СΪ8A��
��2��1��2sʱ���ڻ�·�������ĵ���q�Ĵ�СΪ6C��
��3�����������������ˮƽ����F�������x�Ĺ�ϵʽΪF=��4+4![]() ��N��
��N��
�������������������1����E��tͼ�����t=2sʱ�ĸ�Ӧ�綯�ƣ���ŷķ�����������������ĵ���ǿ��I2�Ĵ�С��
��2�����ݸ�Ӧ����ͼ��������ʾ�������õ�����ƽ��ֵ���������
��3����E=BLv�������������˶���������˶�ѧ��ʽ�õ����ٶȣ�����ţ�ٵڶ��������F�ı���ʽ��
�⣺��1������E��tͼ���е�ͼ���ǹ�ԭ���ֱ���ص㣬�ɵõ�t=2sʱ�����������ĸ�Ӧ�綯��Ϊ��E=4V
��ŷķ���ɵã�
I2=![]() =
=![]() A=8A
A=8A
��2�����ڻ�·�еĵ�����E�����ȣ���֪����I��tͼ���е�ͼ��Ҳ�ǹ�ԭ���ֱ�ߣ����У�t=1sʱ��I1=4A
���У�1��2sʱ���ڻ�·�������ĵ��� q=![]() ��t=
��t=![]() =
=![]() 1C=6C
1C=6C
��3������=45������֪����tʱ�̻�·�е������Ч�и�� L=x
�ٸ���B��xͼ���е�ͼ����˫�����ص��У�
E=BLv=��Bx��v��
��ͼ2��֪��Bx=1��Tm����
��ͼ1֪��E��ʱ������ȣ��� E=2t��V��
��������ʽ�ã�v=2t��m/s��
��֪��������˶����ȼ���ֱ���˶������ٶ� a=2m/s2��
���У�F��=BIL=BIx=��Bx��I����IҲ��ʱ�������
�ٸ���ţ�ٵڶ������У�F��F��=ma
�� x=![]()
������ã�F=��4+4![]() ��N
��N
�𣺣�1��t=2sʱ����������ĵ���ǿ��I2�Ĵ�СΪ8A��
��2��1��2sʱ���ڻ�·�������ĵ���q�Ĵ�СΪ6C��
��3�����������������ˮƽ����F�������x�Ĺ�ϵʽΪF=��4+4![]() ��N��
��N��