题目内容
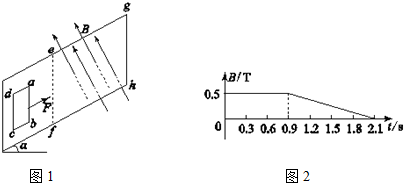
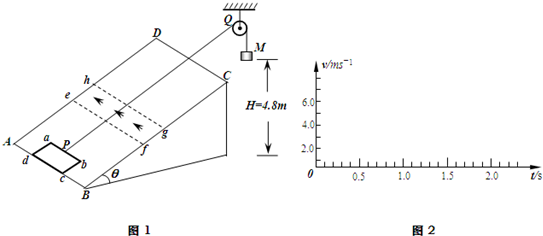
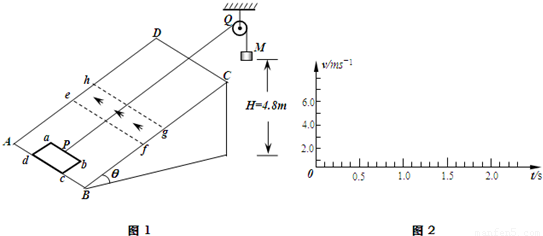
如图1所示,光滑矩形斜面ABCD的倾角θ=30°,在其上放置一矩形金属线框abcd,ab的边长l1=1m,bc的边长l2=0.6m,线框的质量m=1kg,电阻R=0.1Ω,线框通过细线绕过定滑轮与重物相连,细线与斜面平行且靠近;重物质量M=2kg,离地面的高度为H=4.8m;斜面上efgh区域是有界匀强磁场,磁感应强度的大小为0.5T,方向垂直于斜面向上;已知AB到ef的距离为4.2m,ef到gh的距离为0.6m,gh到CD的距离为3.2m,取g=10m/s2;现让线框从静止开始运动(开始时刻,cd边与AB边重合),求:
(1)通过计算,在图2中画出线框从静止开始运动到cd边与CD边重合时(不考虑ab边离开斜面后线框的翻转),线框的速度-时间图象.
(2)线框abcd在整个运动过程中产生的焦耳热.
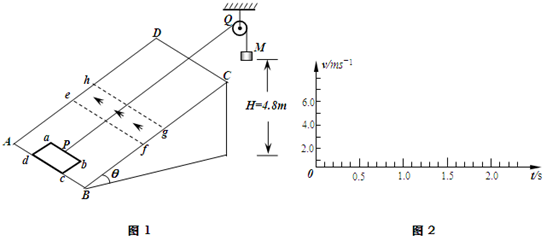
(1)通过计算,在图2中画出线框从静止开始运动到cd边与CD边重合时(不考虑ab边离开斜面后线框的翻转),线框的速度-时间图象.
(2)线框abcd在整个运动过程中产生的焦耳热.

分析:(1)本题要分过程求线框的速度,再作出图象.
首先,线框abcd由静止沿斜面向上运动,到ab与ef线重合过程中,线框和重物以大小相等的加速度做匀加速运动,采用隔离法,由牛顿第二定律求出两个物体的加速度,由运动学公式求出ab恰好要进入磁场时的速度,或根据动能定理列式求ab恰好要进入磁场时的速度.根据计算得知线框进入磁场后做匀速直线运动,直到cd边离开gh的瞬间为止,此时M刚好着地,细绳松弛,线框继续向上做减速运动,再由牛顿第二定律和运动学公式结合求cd边离开CD的速度,即可作出图象.
(2)根据功能关系列式求热量.
首先,线框abcd由静止沿斜面向上运动,到ab与ef线重合过程中,线框和重物以大小相等的加速度做匀加速运动,采用隔离法,由牛顿第二定律求出两个物体的加速度,由运动学公式求出ab恰好要进入磁场时的速度,或根据动能定理列式求ab恰好要进入磁场时的速度.根据计算得知线框进入磁场后做匀速直线运动,直到cd边离开gh的瞬间为止,此时M刚好着地,细绳松弛,线框继续向上做减速运动,再由牛顿第二定律和运动学公式结合求cd边离开CD的速度,即可作出图象.
(2)根据功能关系列式求热量.
解答:解:(1)解法一:
如图所示,线框abcd由静止沿斜面向上运动,到ab与ef线重合过程中,线框受恒力作用,线框和重物以大小相等的加速度做匀加速运动,设为a1,则:
对M:Mg-T=Ma1
对m:T-mgsinθ=ma1
(或对系统直接列出:Mg-mgsinθ=(M+m)a1亦可)
联立得:①、②a1=
=
=5m/s2
设ab恰好要进入磁场时的速度为v0,则:
=2a1s1
解得 v0=
=6m/s
该过程的时间为:t1=
=
=1.2s
ab边刚进入磁场时:Mg-T=Ma2
T-mgsinθ-FA=ma2
又 FA=BIl1 I=
E=Bl1v0
联立求解得:a2=
=
=0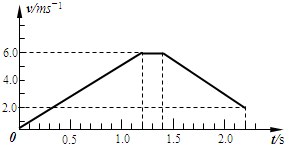
故线框进入磁场后,做匀速直线运动,直到cd边离开gh的瞬间为止,匀速运动的时间 t2=
=
=0.2s
此时M刚好着地,细绳松弛,线框继续向上做减速运动,其加速度大小为:a3=
=gsinθ=5m/s2.
直到线框的cd边离开CD线.设线框cd边离开CD的速度为v1
则得-2a3s2=
-
v1=
=
=2m/s
时间 t3=
=
=0.8s
则线框的速度--时间图象如右图
解法二:
如图所示,线框abcd由静止沿斜面向上运动到ab与ef线重合的过程中,线框和重物在恒力作用下以共同的加速度做匀加速运动.
设ab恰好要进入磁场时的速度为v0,对线框和重物的整体在这一过程运用动能定理:Mgs1-mgs1sinθ=
(M+m)
解得:v0=
=
=6m/s
该过程的时间为:t1=
=
=
=1.2s
ab边刚进入磁场时由于切割磁感线而产生电流,所以线框受到沿斜面向下的安培力作用:FA=BIl1=
故此时,F合=Mg-mgsinθ-FA=20-10×0.5-
=0
故线框进入磁场后,做匀速直线运动,直到cd边离开gh的瞬间为止.t2=
=
=0.2s
此时M刚好着地,细绳松弛,线框继续向上做减速运动,设线框的cd边到达CD线
的速度为v1,则对线框有:-mgs2sinθ=
m
-
m
得v1=
=
=2m/s
t3=
=
=0.8s
则线框的速度--时间图象如右图
(2)解法一:Q=2FAl2=2(Mg-mgsinθ)l2=18J
解法二:Q=Mg?2l2-mg?2l2sinθ=18J
答:
(1)线框的速度-时间图象如图所示.
(2)线框abcd在整个运动过程中产生的焦耳热为18J.
如图所示,线框abcd由静止沿斜面向上运动,到ab与ef线重合过程中,线框受恒力作用,线框和重物以大小相等的加速度做匀加速运动,设为a1,则:
对M:Mg-T=Ma1
对m:T-mgsinθ=ma1
(或对系统直接列出:Mg-mgsinθ=(M+m)a1亦可)
联立得:①、②a1=
| Mg-mgsinθ |
| M+m |
| 20-5 |
| 3 |
设ab恰好要进入磁场时的速度为v0,则:
| v | 2 0 |
解得 v0=
| 2×5×(4.2-0.6) |
该过程的时间为:t1=
| v0-0 |
| a1 |
| 6 |
| 5 |
ab边刚进入磁场时:Mg-T=Ma2
T-mgsinθ-FA=ma2
又 FA=BIl1 I=
| E |
| R |
联立求解得:a2=
MgR-mgRsinθ-B2
| ||
| (M+m)R |
| 20×0.1-5×0.1-0.52×1×6 |
| 3×0.1 |

故线框进入磁场后,做匀速直线运动,直到cd边离开gh的瞬间为止,匀速运动的时间 t2=
| 2l2 |
| v 0 |
| 1.2 |
| 6 |
此时M刚好着地,细绳松弛,线框继续向上做减速运动,其加速度大小为:a3=
| mgsinθ |
| m |
直到线框的cd边离开CD线.设线框cd边离开CD的速度为v1
则得-2a3s2=
| v | 2 1 |
| v | 2 0 |
v1=
|
| 36-2×5×3.2 |
时间 t3=
| v1-v0 |
| -a3 |
| 2-6 |
| -5 |
则线框的速度--时间图象如右图
解法二:
如图所示,线框abcd由静止沿斜面向上运动到ab与ef线重合的过程中,线框和重物在恒力作用下以共同的加速度做匀加速运动.
设ab恰好要进入磁场时的速度为v0,对线框和重物的整体在这一过程运用动能定理:Mgs1-mgs1sinθ=
| 1 |
| 2 |
| v | 2 0 |
解得:v0=
|
|
该过程的时间为:t1=
| s1 | ||
|
| s1 | ||
|
| 4.2-0.6 | ||
|
ab边刚进入磁场时由于切割磁感线而产生电流,所以线框受到沿斜面向下的安培力作用:FA=BIl1=
B2
| ||
| R |
故此时,F合=Mg-mgsinθ-FA=20-10×0.5-
| 0.52×12×6 |
| 0.1 |
故线框进入磁场后,做匀速直线运动,直到cd边离开gh的瞬间为止.t2=
| 2l2 |
| v 0 |
| 1.2 |
| 6 |
此时M刚好着地,细绳松弛,线框继续向上做减速运动,设线框的cd边到达CD线

的速度为v1,则对线框有:-mgs2sinθ=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
得v1=
|
| 36-2×5×3.2 |
t3=
| s2 | ||
|
| 3.2 | ||
|
则线框的速度--时间图象如右图
(2)解法一:Q=2FAl2=2(Mg-mgsinθ)l2=18J
解法二:Q=Mg?2l2-mg?2l2sinθ=18J
答:
(1)线框的速度-时间图象如图所示.
(2)线框abcd在整个运动过程中产生的焦耳热为18J.
点评:本题要能根据线框的受力情况,分析其运动过程,再选择力学和电磁学的规律求解.考查受力平衡条件、能量守恒定律、牛顿第二定律及运动学公式、法拉第定律、欧姆定律、安培力等等众多知识,综合较强.

练习册系列答案
相关题目
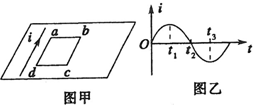 如图甲所示,光滑的水平桌面上固定着一根绝缘的长直导线,可以自由移动的矩形导线框B=1.0T靠近长直导线放在桌面上,当长直导线中的电流按图乙所示的规律变化时(图甲中电流所示的方向为正方向),则( )
如图甲所示,光滑的水平桌面上固定着一根绝缘的长直导线,可以自由移动的矩形导线框B=1.0T靠近长直导线放在桌面上,当长直导线中的电流按图乙所示的规律变化时(图甲中电流所示的方向为正方向),则( )| A、在t2时刻,线框内没有电流,线框不受力 | B、t1到t2时间内,线框内电流的方向为abcda | C、t1到t2时间内,线框向右做匀减速直线运动 | D、t1到t2时间内,线框向左做匀加速直线运动 |