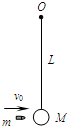题目内容
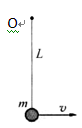
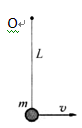
如图所示，悬挂在竖直平面内O点的一个可视为质点的小球，其质量为m，悬线长为L，运动过程中，悬线能承受的最大拉力为F．现给小球一水平初速度v，使其在竖直平面内运动．已知小球在运动时，悬线始终不松弛，试求v的大小范围．分析：分两种情况进行讨论，即小球在运动过程中，最高点与O点等高或比O低时，线不松弛，小球能在竖直平面内做圆周运动，线也不松弛，根据圆周运动的基本公式即可求解．
解答：解：存在两种可能：
（1）小球在运动过程中，最高点与O点等高或比O低时，线不松弛．
mv12≤mgL得：v1≤
（2）小球恰能过最高点时，在最高点速度设为v0，对应的最低点速度设为v2，则有：
解得：v2=
考虑到在运动过程中，悬线又不能断裂，小球在最低点又需满足：
F-mg=m
v2≤
所以，v的大小取值范围为：
0＜v1≤
或
≤v2≤
，在此速度范围，悬线均不会松弛．
答：的大小取值范围为：0＜v1≤
或
≤v2≤
时，悬线均不会松弛．
（1）小球在运动过程中，最高点与O点等高或比O低时，线不松弛．
| 1 |
| 2 |
| 2gL |
（2）小球恰能过最高点时，在最高点速度设为v0，对应的最低点速度设为v2，则有：
|
|
解得：v2=
| 5gL |
考虑到在运动过程中，悬线又不能断裂，小球在最低点又需满足：
F-mg=m
| v22 |
| L |
|
所以，v的大小取值范围为：
0＜v1≤
| 2gL |
| 5gL |
|
答：的大小取值范围为：0＜v1≤
| 2gL |
| 5gL |
|
点评：本题主要考查了圆周运动向心力公式的直接应用，同时要考虑，绳子的拉力不能超过其最大承受力，还要注意有两种情况，难度适中．
练习册系列答案
优加精卷系列答案
相关题目
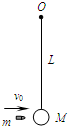如图所示，悬挂在竖直平面内O点的一个木质小球（可以看成质点），悬线长为L，小球的质量为M．一颗质量为m的子弹，以水平速度v0射入木球且留在其中，随即木球就在竖直平面内运动起来．
