题目内容
6.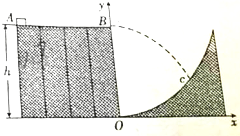 如图所示,在地面上有一固定的水平平台,平台AB长l为1.4m,高h为0.8m,与平台AB间的动摩擦因数μ=0.25,一质量m=0.1kg的物块(可视为质点)从平台的A点以初速度v0为4m/s向B点运动,并水平飞离平台AB并恰好落在呈抛物线形状的坡面上的C点.已知以平台底部边缘的O点为原点建立坐标系Oxy,坡面的抛物线方程为y=1.25x2,忽略空气阻力,重力加速度为g取10m/s2.
如图所示,在地面上有一固定的水平平台,平台AB长l为1.4m,高h为0.8m,与平台AB间的动摩擦因数μ=0.25,一质量m=0.1kg的物块(可视为质点)从平台的A点以初速度v0为4m/s向B点运动,并水平飞离平台AB并恰好落在呈抛物线形状的坡面上的C点.已知以平台底部边缘的O点为原点建立坐标系Oxy,坡面的抛物线方程为y=1.25x2,忽略空气阻力,重力加速度为g取10m/s2.(1)物块运动到B点时的速度大小;
(2)物块落到C点时的动能(结果保留两位有效致字).
分析 (1)对于AB过程由动能定理可求得物块到达B点时的速度;
(2)物体由B点离开后做平抛运动,由平抛运动规律可求得水平和竖直方向上的位移关系;再结合抛物线方程可求解下落时间,再求得竖直分速度即可求得动能.
解答 解:(1)对AB过程由动能定理可知:
-μmgl=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02
解得:v=3m/s;
(2)小球由B点开始做平抛运动,由运动的合成和分解规律可知:
下落高度y0=$\frac{1}{2}$gt2;
水平位移x=vt
则落到C点时,对应的坐标为:y=h-$\frac{1}{2}$gt2;
x=vt
落到C点时,根据抛物线方程可得:
h-$\frac{1}{2}$gt2=1.25(vt)2
解得:
t2=$\frac{8}{162.5}$
则物体到达C点的动能EK=$\frac{1}{2}$mv2+$\frac{1}{2}$mvy2=$\frac{1}{2}$×0.1×9+$\frac{1}{2}$×0.1×102×$\frac{8}{162.5}$=0.70J;
答:(1)物块运动到B点时的速度大小为3m/s;
(2)物体到达C点时的动能为0.70J.
点评 本题考查动能定理和平抛运动的规律,解题的关键在于明确正确应用几何规律,能正确利用对应的函数关系进行分析,从而求出对应的规律;对学生的数学要求较高.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
5. 如图所示,两相同轻质硬杆OO1、OO2可绕其两端垂直纸面的水平轴O、O1、O2转动,在O点悬挂一重物M,将两个相同木块m紧压在竖直挡板上,此时整个系统保持静止.Ff表示木块与挡板间摩擦力的大小,FN表示木块与挡板间正压力的大小.若挡板间的距离稍许增大后,系统仍静止且O1、O2始终等高,则( )
如图所示,两相同轻质硬杆OO1、OO2可绕其两端垂直纸面的水平轴O、O1、O2转动,在O点悬挂一重物M,将两个相同木块m紧压在竖直挡板上,此时整个系统保持静止.Ff表示木块与挡板间摩擦力的大小,FN表示木块与挡板间正压力的大小.若挡板间的距离稍许增大后,系统仍静止且O1、O2始终等高,则( )
 如图所示,两相同轻质硬杆OO1、OO2可绕其两端垂直纸面的水平轴O、O1、O2转动,在O点悬挂一重物M,将两个相同木块m紧压在竖直挡板上,此时整个系统保持静止.Ff表示木块与挡板间摩擦力的大小,FN表示木块与挡板间正压力的大小.若挡板间的距离稍许增大后,系统仍静止且O1、O2始终等高,则( )
如图所示,两相同轻质硬杆OO1、OO2可绕其两端垂直纸面的水平轴O、O1、O2转动,在O点悬挂一重物M,将两个相同木块m紧压在竖直挡板上,此时整个系统保持静止.Ff表示木块与挡板间摩擦力的大小,FN表示木块与挡板间正压力的大小.若挡板间的距离稍许增大后,系统仍静止且O1、O2始终等高,则( )| A. | FN变小 | B. | FN变大 | C. | Ff不变 | D. | Ff变小 |
18. 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L7.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L7.
(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是l5和l6.
(2)实验中,L3和L7两个值还没有测定,请你根据如图将这两个测量值填入上表中.
(3)为了充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm.请你给出第四个差值:d4=7.20cm.
(4)根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{16}$,代入数据解得△L=1.75cm.
(5)计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)
 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L7.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L7.(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是l5和l6.
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值 /cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.1 |
(3)为了充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm.请你给出第四个差值:d4=7.20cm.
(4)根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{16}$,代入数据解得△L=1.75cm.
(5)计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)
15.物体做匀加速直线运动,连续通过A、B、C三点的速度为vA、vB、vC,而且AB与BC间距相等,物体通过AC段时间中间时刻的速度为v,下列说法正确的是( )
| A. | vB=$\frac{{v}_{A+{V}_{C}}}{2}$ | B. | v=$\frac{{v}_{A+}{v}_{C}}{2}$ | C. | vA<vB<v<vC | D. | vA<v<vB<vC |
16. 图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8C的点电荷,沿图中曲线从A点移到B点,电场力做的功为( )
图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8C的点电荷,沿图中曲线从A点移到B点,电场力做的功为( )
 图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8C的点电荷,沿图中曲线从A点移到B点,电场力做的功为( )
图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8C的点电荷,沿图中曲线从A点移到B点,电场力做的功为( )| A. | -5.0×10-7J | B. | 5.0×10-7J | C. | -3.5×10-7J | D. | 3.5×10-7J |
 在追寻科学家研究足迹的过程中,某同学为探究恒力做功和物体动能变化间的关系,采用了如图甲所示的实验装置.
在追寻科学家研究足迹的过程中,某同学为探究恒力做功和物体动能变化间的关系,采用了如图甲所示的实验装置.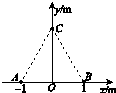 如图所示,真空中xOy平面直角坐标系上的A、B、C三点构成等边三角形,边长L=2.0m.若将电荷量均为q=+2.0×10-6C的两点电荷分别固定在A、B点,已知静电力常量k=9×109 N•m2/C2,求:
如图所示,真空中xOy平面直角坐标系上的A、B、C三点构成等边三角形,边长L=2.0m.若将电荷量均为q=+2.0×10-6C的两点电荷分别固定在A、B点,已知静电力常量k=9×109 N•m2/C2,求: 在电场中一条电场线上有A、B两点,如图所示.若将一负电荷q=2.0×10-7C,从A点移至B点,电荷克服电场力做功4.0×10-4J.试求:
在电场中一条电场线上有A、B两点,如图所示.若将一负电荷q=2.0×10-7C,从A点移至B点,电荷克服电场力做功4.0×10-4J.试求: