题目内容
15.物体做匀加速直线运动,连续通过A、B、C三点的速度为vA、vB、vC,而且AB与BC间距相等,物体通过AC段时间中间时刻的速度为v,下列说法正确的是( )| A. | vB=$\frac{{v}_{A+{V}_{C}}}{2}$ | B. | v=$\frac{{v}_{A+}{v}_{C}}{2}$ | C. | vA<vB<v<vC | D. | vA<v<vB<vC |
分析 根据匀变速直线运动的速度位移公式求出中间位置的速度,根据某段时间内的平均速度等于中间时刻的瞬时速度求出C中间时刻的速度,通过数学方法比较大小.
解答 解:根据速度位移公式得,${{v}_{B}}^{2}-{{v}_{A}}^{2}=2a\frac{x}{2}$,${{v}_{C}}^{2}-{{v}_{B}}^{2}=2a\frac{x}{2}$,联立两式解得${v}_{B}=\sqrt{\frac{{{v}_{A}}^{2}+{{v}_{C}}^{2}}{2}}$,故A错误.
根据平均速度推论知,中间时刻的瞬时速度v=$\frac{{v}_{A}+{v}_{C}}{2}$,故B正确.
根据数学作差法知,${{v}_{B}}^{2}-{v}^{2}=\frac{{{v}_{A}}^{2}+{{v}_{C}}^{2}}{2}-$$\frac{{{v}_{A}}^{2}+{{v}_{C}}^{2}+2{v}_{A}{v}_{C}}{4}$=$\frac{({v}_{A}-{v}_{C})^{2}}{4}>0$,可知vB>v,因为物体做匀加速直线运动,则vA<v<vB<vC.故D正确,C错误.
故选:BD.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,对于比较中间时刻的瞬时速度和中间位置的速度,也可以结合速度时间图线进行求解.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
3.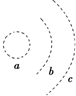 如图所示,a、b、c表示点电荷的电场中三个等势面,它们的电势分别为φa=12V,φb=10V,φc=4V.一带电粒子从等势面a上某处由静止释放后,仅受电场力作用而运动,已知它经过等势面b时的速率为vb,则它经过等势面c时的速率为( )
如图所示,a、b、c表示点电荷的电场中三个等势面,它们的电势分别为φa=12V,φb=10V,φc=4V.一带电粒子从等势面a上某处由静止释放后,仅受电场力作用而运动,已知它经过等势面b时的速率为vb,则它经过等势面c时的速率为( )
 如图所示,a、b、c表示点电荷的电场中三个等势面,它们的电势分别为φa=12V,φb=10V,φc=4V.一带电粒子从等势面a上某处由静止释放后,仅受电场力作用而运动,已知它经过等势面b时的速率为vb,则它经过等势面c时的速率为( )
如图所示,a、b、c表示点电荷的电场中三个等势面,它们的电势分别为φa=12V,φb=10V,φc=4V.一带电粒子从等势面a上某处由静止释放后,仅受电场力作用而运动,已知它经过等势面b时的速率为vb,则它经过等势面c时的速率为( )| A. | 2vb | B. | 4vb | C. | $\sqrt{2}$vb | D. | $\frac{3}{2}$vb |
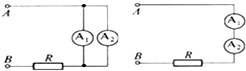 如图所示,A、B两点接在恒压电源上,内阻不可忽略的电流表并联,示数分别为2A和3A.若将两只电流表串联起来接入电路中,两只电流表的示数均为4A,那么电路不接入电流表时,流过R的电流是多少?
如图所示,A、B两点接在恒压电源上,内阻不可忽略的电流表并联,示数分别为2A和3A.若将两只电流表串联起来接入电路中,两只电流表的示数均为4A,那么电路不接入电流表时,流过R的电流是多少?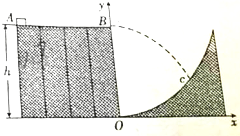 如图所示,在地面上有一固定的水平平台,平台AB长l为1.4m,高h为0.8m,与平台AB间的动摩擦因数μ=0.25,一质量m=0.1kg的物块(可视为质点)从平台的A点以初速度v0为4m/s向B点运动,并水平飞离平台AB并恰好落在呈抛物线形状的坡面上的C点.已知以平台底部边缘的O点为原点建立坐标系Oxy,坡面的抛物线方程为y=1.25x2,忽略空气阻力,重力加速度为g取10m/s2.
如图所示,在地面上有一固定的水平平台,平台AB长l为1.4m,高h为0.8m,与平台AB间的动摩擦因数μ=0.25,一质量m=0.1kg的物块(可视为质点)从平台的A点以初速度v0为4m/s向B点运动,并水平飞离平台AB并恰好落在呈抛物线形状的坡面上的C点.已知以平台底部边缘的O点为原点建立坐标系Oxy,坡面的抛物线方程为y=1.25x2,忽略空气阻力,重力加速度为g取10m/s2.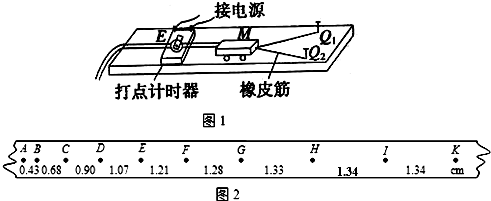
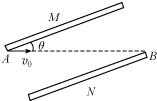 如图所示,倾斜放置的平行板电容器两极板与水平面夹角为θ,极板间距为d,带负电的微 粒质量为m、带电量为q,从极板M的左边缘A处以某一速度vo水平射入,沿直线运动并从极板N的右边缘B处射出,试求:
如图所示,倾斜放置的平行板电容器两极板与水平面夹角为θ,极板间距为d,带负电的微 粒质量为m、带电量为q,从极板M的左边缘A处以某一速度vo水平射入,沿直线运动并从极板N的右边缘B处射出,试求: