��Ŀ����
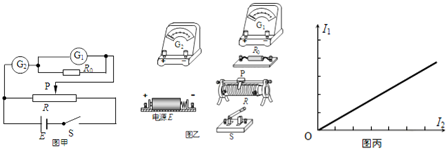
12��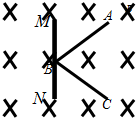 ��ͼ��ʾ��ABC�ǹ̶��ھ�Եˮƽ���ϵĹ⻬�������죬����AB=BC=L���н�Ϊ60�㣬�ҵ�λ���ȵĵ����Ϊr�����촦�ڴŸ�Ӧǿ�ȴ�СΪB������ֱֽ���������ǿ�ų��У�MN��һ�������ˣ����ȴ���L��������Բ��ƣ���MN���������������ٶ�v0��ABC�����ٻ��У�ʼ���뵼��Ӵ����ã�������ACȷ����ֱ�߱���ƽ�У���1���ڵ����ϻ��й�����MN�ܰ�����F�뻬��λ��x�Ĺ�ϵ����ʽ������F-xͼ��
��ͼ��ʾ��ABC�ǹ̶��ھ�Եˮƽ���ϵĹ⻬�������죬����AB=BC=L���н�Ϊ60�㣬�ҵ�λ���ȵĵ����Ϊr�����촦�ڴŸ�Ӧǿ�ȴ�СΪB������ֱֽ���������ǿ�ų��У�MN��һ�������ˣ����ȴ���L��������Բ��ƣ���MN���������������ٶ�v0��ABC�����ٻ��У�ʼ���뵼��Ӵ����ã�������ACȷ����ֱ�߱���ƽ�У���1���ڵ����ϻ��й�����MN�ܰ�����F�뻬��λ��x�Ĺ�ϵ����ʽ������F-xͼ����2������ȫ�����й��ɻ�·�������Ľ�����Q��ͨ��B�����ĵ���q��
���� ��1��MN�и�Ÿ��ߣ����÷����ڵ�Ÿ�Ӧ���������Ӧ�綯�Ƶı���ʽ��Ӧ�ñպϵ�·ŷķ���������Ӧ�����ı���ʽ���ɹ�ʽF=BIL��ⰲ����F��x�ı���ʽ���ٻ���ͼ��
��2����ͼ����˷��������������ɹ��ܹ�ϵ�����·�������Ľ����ȣ���·�и�Ӧ�������䣬��q=It�����q��
��� �⣺��1�����о���xʱ�����˲����ĸ�Ӧ�綯��Ϊ
E=B��2xtan30�㣩v0=$\frac{2\sqrt{3}}{3}$Bxv0��
�պϻ�·���ܵ��� R=$\frac{2x}{cos30��}$r=$\frac{4\sqrt{3}}{3}$xr
�������ϵİ����� $F=B\frac{E}{R}��2xtan30�㣩=\frac{{\sqrt{3}{B^2}{v_0}}}{3r}x$$��0��x��\frac{{\sqrt{3}}}{2}L��$
ͼ����ͼ
��2����ͼ��Χ�ɡ��������ʾ�����˿˷����������������ڻ�·�����Ľ����ȣ�����Ϊ Q=$\frac{1}{2}��\frac{\sqrt{3}}{2}L��\frac{{B}_{0}^{2}{v}_{0}L}{2r}$=$\frac{\sqrt{3}{B}^{2}{v}_{0}{L}^{2}}{8r}$
��·�е��� $I=\frac{{B{V_0}}}{2r}$$t=\frac{{\frac{{\sqrt{3}}}{2}L}}{V_0}$�����ֲ���
��ͨ��B�����ĵ��� $q=It=\frac{{\sqrt{3}BL}}{4r}$
��
��1���ڵ����ϻ��й�����MN�ܰ�����F�뻬��λ��x�Ĺ�ϵ����ʽΪF=$\frac{\sqrt{3}{B}^{2}{v}_{0}}{3r}$x��0��x��$\frac{\sqrt{3}}{2}$L��������F-xͼ����ͼ��
��2������ȫ�����й��ɻ�·�������Ľ�����QΪ$\frac{\sqrt{3}{B}^{2}{v}_{0}{L}^{2}}{8r}$��ͨ��B�����ĵ���q��$\frac{\sqrt{3}BL}{4r}$��
���� �����ʱҪע������˵ĵ��費�ƣ��������е��裬���ҵ�����x�DZ仯���ܸ��������������������֮��Ĺ�ϵ���Ӷ�����ͼ��

 ��ͼ��һ��������С������Ϊm����˿��������O�㣬������ֱƽ���ڰڶ������ڽ�Ϊ60�㣬ˮƽ�ų���ֱ��С��ڶ���ƽ�森��С�����ڵ���͵�ʱ�������ϵ�����ǡΪ�㣬��С�����ҷ����ڽǴ��ڵ���͵�˵����ȷ���ǣ�������
��ͼ��һ��������С������Ϊm����˿��������O�㣬������ֱƽ���ڰڶ������ڽ�Ϊ60�㣬ˮƽ�ų���ֱ��С��ڶ���ƽ�森��С�����ڵ���͵�ʱ�������ϵ�����ǡΪ�㣬��С�����ҷ����ڽǴ��ڵ���͵�˵����ȷ���ǣ�������| A�� | С����ܴ����� | |
| B�� | �����ϵ�����ҲΪ0 | |
| C�� | �����ϵ�����Ϊ4mg | |
| D�� | С���������ڵ���͵�ʱ������ͬ |
 ��ͼ��ʾ�������Ϊ30��Ĺ⻬б���ϣ����ɵ��϶˹̶���б�涥�ˣ��¶˸�����Ϊm��С����������F=2mg������������������ҲΪm��������ϼ�ѹС������ϵͳ���ھ�ֹ״̬����ͻȻ��ȥ����F���ڳ�ȥ������˲�䣬����˵����ȷ���ǣ�������
��ͼ��ʾ�������Ϊ30��Ĺ⻬б���ϣ����ɵ��϶˹̶���б�涥�ˣ��¶˸�����Ϊm��С����������F=2mg������������������ҲΪm��������ϼ�ѹС������ϵͳ���ھ�ֹ״̬����ͻȻ��ȥ����F���ڳ�ȥ������˲�䣬����˵����ȷ���ǣ�������| A�� | С��ļ��ٶ�Ϊ�� | |
| B�� | ���ļ��ٶ�Ϊg | |
| C�� | С������֮������������СΪ0.5mg | |
| D�� | С������֮����������Ϊ�� |
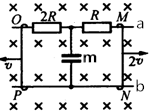 ��ͼ��ʾ��װ����a��b������ƽ��ֱ���죬MN��OP�Ǵ�ֱ����a��b�ϲ������һ���������ƽ��ֱ���ߣ�ÿ����Ϊl�������Ͻ�����ֵ�ֱ�ΪR��2R�����������һ���峤ΪL�䡢���Ϊd��ƽ�а����������Ŀ��û�����������װ�÷��ڴŸ�Ӧǿ��ΪB��ֱ����ƽ�����ǿ�ų��У���������ʹMN������2v�������ٻ�����OP������v�������ٻ���ʱ����ƽ�а�������������һ������Ϊm�Ĵ�����ǡ��ƽ�⣬���ʣ�
��ͼ��ʾ��װ����a��b������ƽ��ֱ���죬MN��OP�Ǵ�ֱ����a��b�ϲ������һ���������ƽ��ֱ���ߣ�ÿ����Ϊl�������Ͻ�����ֵ�ֱ�ΪR��2R�����������һ���峤ΪL�䡢���Ϊd��ƽ�а����������Ŀ��û�����������װ�÷��ڴŸ�Ӧǿ��ΪB��ֱ����ƽ�����ǿ�ų��У���������ʹMN������2v�������ٻ�����OP������v�������ٻ���ʱ����ƽ�а�������������һ������Ϊm�Ĵ�����ǡ��ƽ�⣬���ʣ�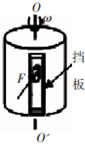 ��һ�뾶r=0.2m��Բ��������ֱ��OO���Խ��ٶȦ�=9rad/s����ת����������F������m=1kg������A��ֱѹ��Բ����IJ��棬�����ܹ⻬��������ã�����A��ˮƽ�����ϲ�����Բ����ת��������v0=2.4m/s�����������»���������A��Բ����֮��Ķ�Ħ��������=0.25����
��һ�뾶r=0.2m��Բ��������ֱ��OO���Խ��ٶȦ�=9rad/s����ת����������F������m=1kg������A��ֱѹ��Բ����IJ��棬�����ܹ⻬��������ã�����A��ˮƽ�����ϲ�����Բ����ת��������v0=2.4m/s�����������»���������A��Բ����֮��Ķ�Ħ��������=0.25����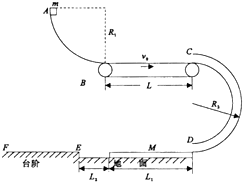 ��ͼ��ʾ����L=4mˮƽ���ʹ���vo=6m/s���ٶ�˳ʱ������ת���������һ�뾶ΪR1=0.8m��$\frac{1}{4}$�⻬Բ����Բ���ײ���Ƥ����ͬһˮƽ���ϣ��Ҳ���һ�뾶ΪR2=0.8m�İ�Բ�⻬ϸ�ܣ�Բ���϶˿��²����ý���Ƥ������Ƥ����ͬһˮƽ���ϣ��⻬ˮƽ�����Ͻ����ܿ���һ����ΪL1=9m������ΪM=6kg��ľ�壬ľ���϶�������ܿڵײ���ͬһˮƽ���ϣ�ľ�������һ�㹻����̨�ף���߶�������ľ����ͬ��ľ�������̨����ΪL2=lm����ľ����̨����ײʱ������ճס�ٶȱ�Ϊ�㣮�ֽ�һ����Ϊm=2kg������$\frac{1}{4}$�⻬Բ���Ķ���A�ɾ�ֹ�ͷţ���֪Ƥ��������Ķ�Ħ������Ϊu1=
��ͼ��ʾ����L=4mˮƽ���ʹ���vo=6m/s���ٶ�˳ʱ������ת���������һ�뾶ΪR1=0.8m��$\frac{1}{4}$�⻬Բ����Բ���ײ���Ƥ����ͬһˮƽ���ϣ��Ҳ���һ�뾶ΪR2=0.8m�İ�Բ�⻬ϸ�ܣ�Բ���϶˿��²����ý���Ƥ������Ƥ����ͬһˮƽ���ϣ��⻬ˮƽ�����Ͻ����ܿ���һ����ΪL1=9m������ΪM=6kg��ľ�壬ľ���϶�������ܿڵײ���ͬһˮƽ���ϣ�ľ�������һ�㹻����̨�ף���߶�������ľ����ͬ��ľ�������̨����ΪL2=lm����ľ����̨����ײʱ������ճס�ٶȱ�Ϊ�㣮�ֽ�һ����Ϊm=2kg������$\frac{1}{4}$�⻬Բ���Ķ���A�ɾ�ֹ�ͷţ���֪Ƥ��������Ķ�Ħ������Ϊu1=