题目内容
17.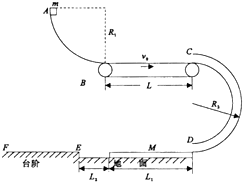 如图所示,长L=4m水平传送带以vo=6m/s的速度顺时针匀速转动,左侧有一半径为R1=0.8m的$\frac{1}{4}$光滑圆弧,圆弧底部与皮带在同一水平线上,右侧有一半径为R2=0.8m的半圆光滑细管,圆管上端口下部正好紧邻皮带且与皮带在同一水平线上,光滑水平地面上紧靠管口有一长度为L1=9m、质量为M=6kg的木板,木板上端正好与管口底部在同一水平线上,木板的左方有一足够长的台阶,其高度正好与木板相同,木板左侧与台阶距离为L2=lm,当木板与台阶碰撞时立即被粘住速度变为零.现将一质量为m=2kg的物块从$\frac{1}{4}$光滑圆弧的顶部A由静止释放,已知皮带与物块间的动摩擦因数为u1=
如图所示,长L=4m水平传送带以vo=6m/s的速度顺时针匀速转动,左侧有一半径为R1=0.8m的$\frac{1}{4}$光滑圆弧,圆弧底部与皮带在同一水平线上,右侧有一半径为R2=0.8m的半圆光滑细管,圆管上端口下部正好紧邻皮带且与皮带在同一水平线上,光滑水平地面上紧靠管口有一长度为L1=9m、质量为M=6kg的木板,木板上端正好与管口底部在同一水平线上,木板的左方有一足够长的台阶,其高度正好与木板相同,木板左侧与台阶距离为L2=lm,当木板与台阶碰撞时立即被粘住速度变为零.现将一质量为m=2kg的物块从$\frac{1}{4}$光滑圆弧的顶部A由静止释放,已知皮带与物块间的动摩擦因数为u1=0.2,物块与木板间的动摩擦因数u2=0.3,物块与台阶表面的动摩擦因数也为u2=0.3,g=l0m/s2,物块可视为质点,圆管粗细不计,试求:
(1)物块刚滑人圆管顶部C处的速度大小;
(2)物块滑到圆管底部D处对底部的压力;
(3)判断物块最终停在何处.
分析 (1)根据机械能守恒求出物块下滑到B点的速度,分析物块在传送带上的运动规律,根据动能定理求出物块刚滑人圆管顶部C处的速度大小.
(2)根据机械能守恒定律求出物块到达D处的速度,结合牛顿第二定律求出支持力的大小,从而得出物块对底部压力的大小.
(3)物块滑上木板后做匀减速运动,木板做匀加速运动,由牛顿第二定律求两者的加速度,由速度时间公式求出两者速度所用时间和共同速度,求出此过程木板通过的位移,从而分析两者速度能否相等.当木板被粘住后,木块继续滑行设滑上台阶运动,由动能定理求出物块在平台上滑行的距离,即可求解.
解答 解:(1)物块下滑到B点时的速度为v1,由机械能守恒可得:
mgR1=$\frac{1}{2}$m1v12
代入数据解得:v1=4m/s
因为v0=6m/s>v1=4m/s,故物块滑上皮带后做匀加速运动,若一直加速由动能定理得:
μ1mgL=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12
代入数据解得:v2=4$\sqrt{2}$m/s<v0=6m/s
故物块一直匀加速,则滑块以v2=4$\sqrt{2}$m/s滑入管口.
(2)由C点到D点由机械能守恒定律可得:
$\frac{1}{2}$mv22+mg•2R=$\frac{1}{2}$mv32;
在D处,由牛顿第二运动定律:FN-mg=m$\frac{{v}_{3}^{2}}{R}$
代入数据解得:FN=180N
由牛顿第三运动定律可得:FN′=FN=180N
(3)物块滑上木板后最终共速为v4,由牛顿第二运动定律:
μ2mg=ma1;
μ2mg=Ma2;
由运动学公式可得:
v3-a1t=a2t
可得共速速度 v4=a2t=2m/s,水平向左
此过程物块运动的位移为x1,木板运动的位移为x2,由动能定理得:
对物块有:μ2mgx1=$\frac{1}{2}m{v}_{4}^{2}$-$\frac{1}{2}m{v}_{3}^{2}$
对木板有:μ2mgx2=$\frac{1}{2}M{v}_{4}^{2}$
解得:x1=10m,x2=2m
由于x1-x2=8m<L1,两者共速需要木板运动x2=2m>L2.因此物块与木板不能共速.
当木板被粘住后,木块继续滑行设滑上台阶运动x3后停止
由动能定理得:μ2mg(L1+L2+x3)=0-$\frac{1}{2}m{v}_{3}^{2}$
解得:x3=$\frac{2}{3}$m,即离台阶右侧E点为$\frac{2}{3}$m处停下.
答:(1)物块刚滑人圆管顶部C处的速度大小是4$\sqrt{2}$m/s;
(2)物块滑到圆管底部D处对底部的压力是180N;
(3)物块最终在离台阶右侧E点为$\frac{2}{3}$m处停下.
点评 解决本题的关键要正确分析物块的运动过程,把握每个过程所遵守的物理规律,明确物块与木板速度相同这一临界状态,边计算边分析判断.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 0 N | B. | 1 N | C. | 12 N | D. | 23 N |
| A. |  | B. | 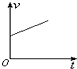 | C. | 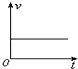 | D. |  |
| A. | 物体的重心位置跟物体的质量分布情况和物体的形状有关 | |
| B. | 用线悬挂的物体静止时,细线方向一定通过重心 | |
| C. | 同一物体在地球表面附近无论向上或向下运动都受重力 | |
| D. | 重力是由于物体受到地球的吸引而产生的 |
 中的线圈的电阻率,某实验小组的部分实验方案如下:
中的线圈的电阻率,某实验小组的部分实验方案如下: (0~3A,约5Ω);
(0~3A,约5Ω); (0~30mA,约10Ω);
(0~30mA,约10Ω);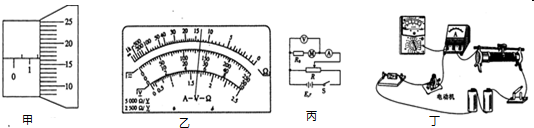
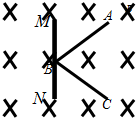 如图所示,ABC是固定在绝缘水平面上的光滑金属导轨,长度AB=BC=L,夹角为60°,且单位长度的电阻均为r,导轨处于磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,MN是一根金属杆,长度大于L,电阻忽略不计.现MN在外力作用下以速度v0在ABC上匀速滑行,始终与导轨接触良好,并且与AC确定的直线保持平行.求:(1)在导轨上滑行过程中MN受安培力F与滑行位移x的关系表达式并画出F-x图象;
如图所示,ABC是固定在绝缘水平面上的光滑金属导轨,长度AB=BC=L,夹角为60°,且单位长度的电阻均为r,导轨处于磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,MN是一根金属杆,长度大于L,电阻忽略不计.现MN在外力作用下以速度v0在ABC上匀速滑行,始终与导轨接触良好,并且与AC确定的直线保持平行.求:(1)在导轨上滑行过程中MN受安培力F与滑行位移x的关系表达式并画出F-x图象; 如图所示,物体A、B的重力分别为GA、GB均处于静止状态,不计滑轮与绳的摩擦,求地面对A的支持力和摩擦力.(α已知)
如图所示,物体A、B的重力分别为GA、GB均处于静止状态,不计滑轮与绳的摩擦,求地面对A的支持力和摩擦力.(α已知) 一绝缘U形杆由两段相互平行的足够长的直杆PQ、MN和一半径为R的光滑半圆环MAP组成,固定在竖直平面内,其中MN杆是光滑的,PQ杆是粗糙的,现将一质量为m的带正电荷的小环(重力大于摩擦力)套在MN上.将小环由D点静止释放,如图所示.
一绝缘U形杆由两段相互平行的足够长的直杆PQ、MN和一半径为R的光滑半圆环MAP组成,固定在竖直平面内,其中MN杆是光滑的,PQ杆是粗糙的,现将一质量为m的带正电荷的小环(重力大于摩擦力)套在MN上.将小环由D点静止释放,如图所示.