题目内容
【题目】如图所示,在竖直xOy平面内0≤x≤L的区域存在沿x轴正方向的句强电场,场强大小为E,垂直向里的匀强磁场,磁感应强度大小为B;在L≤x≤2L的区域存在沿y轴正方向的匀强电场,场强大小也为E,垂直向外的匀强磁场,磁感应强度大小也为B;在2L≤x≤3L的区域存在沿y轴正方向的匀强电场,场强大小为2E。一个质量为m,带电量为+q的带电小球从坐标原点以速度v沿与x轴成45°射入,小球沿直线穿过0≤x≤L区域,在L≤x≤2L的区域运动一段时间后,垂直电场进入2L≤x≤3L区域。已知L、m、q、v,重力加速度g未知,试求:
(1)磁感应强度B和电场强度E的大小;
(2)小球离开电场的位置坐标。

【答案】(1)![]() ,
,![]() ;(2)
;(2)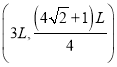
【解析】
(1)带电小球在![]() 区域作匀速直线运动,对其受力分析如图,可知
区域作匀速直线运动,对其受力分析如图,可知
![]()
且
![]()
带电小球在![]() 区域做匀速圆周运动,其轨迹如图所示,轨迹半径为R
区域做匀速圆周运动,其轨迹如图所示,轨迹半径为R
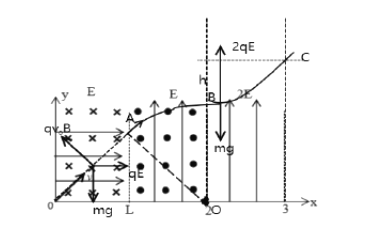
由几何关系可知
![]()
由洛伦兹力提供向心力
![]()
联立解得
![]() ,
,![]()
(2)带电小球在![]() 区域受力分析如图,向上做类平抛运动,运动轨迹如图
区域受力分析如图,向上做类平抛运动,运动轨迹如图
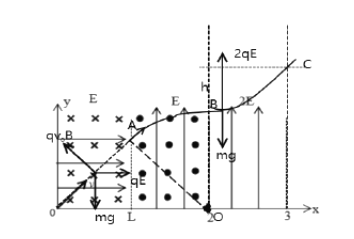
在![]() 运动时间为t,则有
运动时间为t,则有
![]()
类平抛运动的加速度为a,根据牛顿第二定律
![]()
竖直方向偏转位移为h,则有
![]()
小球离开电场的竖起高度为y,则有
![]()
联立解得
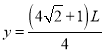
则小球离开电场的位置坐标为
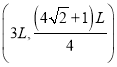

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】甲乙两同学探究做圆周运动的物体所受向心力大小。


(1)甲同学利用细绳系一小物体在空气中甩动,使物体在水平面内做圆周运动,来感受向心力大小,则下列说法中正确的是__________
A.保持质量、绳长不变,增大转速,绳对手的拉力将不变
B.保持质量、绳长不变,增大转速,绳对手的拉力将增大
C.保持质量、角速度不变,增大绳长,绳对手的拉力将不变
D.保持质量、角速度不变,增大绳长,绳对手的拉力将增大
(2)乙同学利用如图甲所示的实验装置,探究做圆周运动的物体所受向心力大小与质量、轨道半径及线速度的定量关系。圆柱体放置在水平光滑圆盘(图中未画出)上做匀速圆周运动,力电传感器测定的是向心力,光电传感器测定的是圆柱体的线速度,该同学通过保持圆柱体质量和运动半径不变,来探究向心力F与线速度v的关系:
①该同学采用的实验方法为__________
A.等效替代法
B.控制变量法
C.理想化模型法
D.微小量放大法
②改变线速度v,多次测量,该同学测出了五组F、v数据,如下表所示,请在图乙中作出F-v2图线__________;
v/ms-1 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
v2/m2s-2 | 1.0 | 2.25 | 4.0 | 6.25 | 9.0 |
F/N | 0.90 | 2.00 | 3.60 | 5.60 | 8.10 |
③由作出的F-v2的图线,可得出F和v2的关系式:__________,若圆柱体运动半径r=0.4m,得圆柱体的质量m=_______________kg。(结果保留两位有效数字)


