题目内容
一星球密度和地球密度相同,它的表面重力加速度是地球表面重力加速度的2倍,则该星球质量是地球质量的( )A.2倍
B.4倍
C.8倍
D.16倍
【答案】分析:根据万有引力等于重力,列出等式表示出重力加速度.
根据密度与质量关系代入表达式找出半径的关系,再求出质量关系.
解答:解:根据万有引力等于重力,列出等式:
 =mg
=mg
g=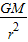 ,其中M是地球的质量,r应该是物体在某位置到球心的距离.
,其中M是地球的质量,r应该是物体在某位置到球心的距离.
根据根据密度与质量关系得:M=ρ? πr3,星球的密度跟地球密度相同,
πr3,星球的密度跟地球密度相同,
g= =ρ?
=ρ? πr,
πr,
星球的表面重力加速度是地球表面重力加速度的2倍,所以星球的半径也是地球的2倍,
所以再根据M=ρ? πr3得:星球质量是地球质量的8倍.
πr3得:星球质量是地球质量的8倍.
故选C.
点评:求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再根据表达式进行比较.
根据密度与质量关系代入表达式找出半径的关系,再求出质量关系.
解答:解:根据万有引力等于重力,列出等式:
 =mg
=mgg=
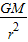 ,其中M是地球的质量,r应该是物体在某位置到球心的距离.
,其中M是地球的质量,r应该是物体在某位置到球心的距离.根据根据密度与质量关系得:M=ρ?
 πr3,星球的密度跟地球密度相同,
πr3,星球的密度跟地球密度相同,g=
 =ρ?
=ρ? πr,
πr,星球的表面重力加速度是地球表面重力加速度的2倍,所以星球的半径也是地球的2倍,
所以再根据M=ρ?
 πr3得:星球质量是地球质量的8倍.
πr3得:星球质量是地球质量的8倍.故选C.
点评:求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再根据表达式进行比较.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目