题目内容
12. 一辆汽车以25m/s的速率在某校区匀速行驶,当这辆违章超速行驶的汽车刚刚超过一辆警车时,警车立即从静止以2.5m/s2的加速度追去.
一辆汽车以25m/s的速率在某校区匀速行驶,当这辆违章超速行驶的汽车刚刚超过一辆警车时,警车立即从静止以2.5m/s2的加速度追去.(1)试在同一坐标中画出汽车和警车的v-t图.
(2)警车何时能截获超速车.
(3)警车截获超速车时,警车的速度为多大?
(4)何时两车距离最远?
分析 做匀加速直线运动,速度时间图线是过原点的倾斜直线,斜率的大小等于加速度.汽车做匀速直线运动,速度时间图线是平行于时间轴的一条直线.
(2)警车追上超速车时,两车的位移相等,根据运动学公式,抓住位移相等,求出追及的时间.
(3)求出追及的时间,根据v=at求出警车截获超速车时的速度
(4)追上前两车速度相等时两车相距最远,根据速度时间关系和位移时间关系分别求解即可.
解答 解:(1)汽车匀速行驶,图象是平行于时间轴的直线,警车初速度为零的匀加速直线运动图象是过原点的倾斜的直线;
(2)根据位移相等时警车截获汽车有:
$\frac{1}{2}a{t}^{2}=vt$
可得时间t=$\frac{2v}{a}=\frac{2×25}{2.5}s=20s$
(2)截获汽车时警车的速度v′=at=2.5×20m/s=50m/s
(3)截获前两车速度相等时两车相距最远有:
v=at′
可得时间t$′=\frac{v}{a}=\frac{25}{2.5}s=10s$
此过程中两车相距$△x=vt′-\frac{1}{2}at{′}^{2}=25×10-\frac{1}{2}×2.5×1{0}^{2}m$=125m
答:(1)图如解答所示;
(2)警车20s后能截获超速车.
(3)警车截获超速车时,警车的速度为50m/s;
(4)警车启动后10s两车距离最远.
点评 在求追及时间时,关键抓住两车的位移相等,运用运动学公式进行求解,两车相距最远的临界条件是两车速度相等.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
3.如图为一条电场线,可以判定( )


| A. | 该电场一定是匀强电场 | |
| B. | 点A处的场强大于点B处的场强 | |
| C. | 点A处的场强小于于点B处的场强 | |
| D. | 负电荷放在B点时所受电场力方向向左 |
7.为了安全,在公路上行驶的汽车之间应保持必要的距离.已知某汽车的速度v=108km/h.假设前方车辆突然停止,汽车司机从发现这一情况,经操纵刹车,到汽车开始减速所经历的时间(即反应时间)t=0.50s.刹车时汽车加速度的大小为4.0m/s2,则两车间的距离s至少应为( )
| A. | 15m | B. | 112..5m | C. | 97.5m | D. | 127.5m |
1.一辆汽车保持恒定速率驶过一座圆弧形拱桥,在此过程中( )

| A. | 汽车做匀速运动 | B. | 汽车做匀变速运动 | ||
| C. | 汽车所受合力不变 | D. | 汽车加速度大小恒定 |

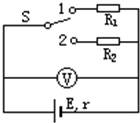 在图所示的电路中,电源的内阻不能忽略.已知定值电阻R1=9Ω,R2=4Ω.当单刀双掷开关S置于位置1时,电压表读数为2.7V.则当S置于位置2时,电压表读数为2.4V.求:电源的电动势E和内阻r.
在图所示的电路中,电源的内阻不能忽略.已知定值电阻R1=9Ω,R2=4Ω.当单刀双掷开关S置于位置1时,电压表读数为2.7V.则当S置于位置2时,电压表读数为2.4V.求:电源的电动势E和内阻r. 一列简谐波沿x轴正方向传播,在t=0时刻的波形如图所示,已知波的速度为10m/s.则t=0.2s时刻正确的波形应是下图中的( )
一列简谐波沿x轴正方向传播,在t=0时刻的波形如图所示,已知波的速度为10m/s.则t=0.2s时刻正确的波形应是下图中的( )


