题目内容
8.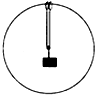 一根长为2R且不可伸长的轻绳两端分別系在质量为m的小圆环上,小圆环静置于半径为R的大圆环的顶端A点.在绳上通过一个光滑挂钩悬挂一质量为M=2m的小物块.由于某种扰动,两小圆环分别向两边对称地缓慢移动,则在此过程中下列说法正确的有( )
一根长为2R且不可伸长的轻绳两端分別系在质量为m的小圆环上,小圆环静置于半径为R的大圆环的顶端A点.在绳上通过一个光滑挂钩悬挂一质量为M=2m的小物块.由于某种扰动,两小圆环分别向两边对称地缓慢移动,则在此过程中下列说法正确的有( )| A. | 小圆环受到的支持力逐渐增大 | |
| B. | 小圆环受到的摩擦力逐渐减小 | |
| C. | 轻绳中的张力逐渐变大 | |
| D. | 如果小环与大环之间光滑,轻绳都可以成水平拉直状态 |
分析 两小圆环分别向两边对称地缓慢移动到某点时,小圆环和物块都受力平衡,对其中一个圆环和小物块受力分析,根据共点力平衡条件列式结合几何关系求解即可.
解答 解:A、两小圆环分别向两边对称地缓慢移动到B点时,对其中一个圆环和小物块受力分析,如图所示:
设绳与竖直方向的夹角为θ,物体处于平衡状态,根据平衡条件得:
T=$\frac{Mg}{2cosθ}=\frac{2mg}{2cosθ}=\frac{mg}{cosθ}$,θ增大,cosθ减小,则T增大,
小圆环处于平衡状态,则有:
f=mgsinθ,θ增大,sinθ增大,则f增大,
N=T+mgcosθ=mg(cosθ+$\frac{1}{cosθ}$),当cosθ=$\frac{1}{cosθ}$时,N最大,所以小环受到的支持力先增大,后减小,故AB错误,C正确;
D、若轻绳都成水平拉直状态,对M受力分析可知,M不能受力平衡,故D错误.
故选:C
点评 本题是共点力平衡中动态变化分析问题,关键在于运用几何知识分析绳子与竖直方向夹角的变化,这在高考中曾经出现过,有一定的难度.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | 质点和重心都是理想化模型 | |
| B. | 牛顿第一定律是牛顿第二定律的特例 | |
| C. | 牛顿发现了万有引力定律.并预言了太阳系各行星的运动轨道 | |
| D. | 速度和加速度都是采用比值法定义的物理量 |
13.铀是常用的一种核燃料,若它的原子核发生了如下的裂变反应:$\left.\begin{array}{l}{235}\\{92}\end{array}\right.$U+$\left.\begin{array}{l}{1}\\{0}\end{array}\right.$n→a+b+2$\left.\begin{array}{l}{1}\\{0}\end{array}\right.$n,则a+b可能是( )
| A. | $\left.\begin{array}{l}{140}\\{54}\end{array}\right.$Xe+$\left.\begin{array}{l}{93}\\{36}\end{array}\right.$Kr | B. | $\left.\begin{array}{l}{141}\\{56}\end{array}\right.$Ba+$\left.\begin{array}{l}{92}\\{36}\end{array}\right.$Kr | ||
| C. | $\left.\begin{array}{l}{141}\\{56}\end{array}\right.$Ba+$\left.\begin{array}{l}{93}\\{38}\end{array}\right.$Sr | D. | $\left.\begin{array}{l}{140}\\{54}\end{array}\right.$Xe+$\left.\begin{array}{l}{94}\\{38}\end{array}\right.$Sr |


 (1)用如图所示表盘的多用电表正确测量了一个3000Ω的电阻后,需要继续测量一个 标称为(220V,100W)的白炽灯泡.在用红、黑表笔接触这个白炽灯泡两端之前,以下哪些操作步骤是必须的?请选择其中合理的操作步骤:CBE
(1)用如图所示表盘的多用电表正确测量了一个3000Ω的电阻后,需要继续测量一个 标称为(220V,100W)的白炽灯泡.在用红、黑表笔接触这个白炽灯泡两端之前,以下哪些操作步骤是必须的?请选择其中合理的操作步骤:CBE