��Ŀ����
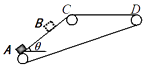
����Ŀ����ͼ��ʾ���뾶ΪR��δ֪���Ĺ⻬��Բ���ABC�����Ϊ��=37���Ĵֲ�б����DC������C��Բ�����ֱ��AC��б�洹ֱ������Ϊm��С���A�����Ϸ���A��Ϊh��б���Ϸ�P����ijһ�ٶ�ˮƽ�׳����պ����Բ�����A�����н����Բ����ڲ���֮��Բ�����б��պû������׳���ȸߵ�D������֪���ص��������ٶ�Ϊg��sin37��=0.6��cos37��=0.8�����ƿ�������������

(1)С���׳�ʱ���ٶ�v0��
(2)С���C��D������Ħ���������Ĺ�Wf��
���𰸡���1��![]() ��2��
��2��![]()
�����������������С���P��A������ƽ���˶������˶�ѧ��ʽ���С��A��ʱ��ֱ������ٶȣ������ٶȷֽ�ͼ���������С���׳�ʱ���ٶ�v0�����������˶����̣���������Ϊ�㣬���ݶ��ܶ������С���C��D������Ħ�������Ĺ�Wf��
��1��С��A��ʱ���ٶ���ˮƽ����ļн�Ϊ������ͼ��ʾ��
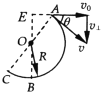
�����ٶ�λ�ƹ�ʽ�� ![]()
�ɼ��ι�ϵ�ã� ![]()
��ã� ![]()
��2�������˶�֪�����У���������Ϊ�㣬���ݶ��ܶ�����֪��С����б���ϻ������п˷�Ħ�������Ĺ�����С����ƽ���˶��ij����ܣ����У� ![]()

��ϰ��ϵ�д�
 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
�����Ŀ