题目内容
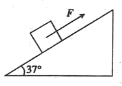
【题目】如图所示,质量m=lkg的物块,在沿斜面向上、大小F=15N的拉力作用下,沿倾角![]() 的足够长斜面由静止开始匀加速上滑,经时间
的足够长斜面由静止开始匀加速上滑,经时间![]() 撤去拉力。已知物块与斜面间的动摩擦因数
撤去拉力。已知物块与斜面间的动摩擦因数![]() ,取
,取![]() ,
, ![]() ,求:
,求:
(1)拉力F作用的时间![]() 内,物块沿斜面上滑的距离
内,物块沿斜面上滑的距离![]() ;
;
(2)从撤去拉力起,物块沿斜面滑到最高点的时间![]() ;
;
(3)从撤去拉力起,经时间t=3s物块到出发点的距离x。
【答案】(1)10m,(2)ls,(3)11m.
【解析】试题分析:(1)物块上滑时,分析受力,运用牛顿第二定律求得加速度,再由位移公式求物块沿斜面上滑的距离![]() ;(2)结合匀变速直线运动的速度公式求出撤去F时物体的速度大小;撤去拉力后物体先做匀减速直线运动至速度减为零,利用牛顿第二定律和速度公式结合求时间时间
;(2)结合匀变速直线运动的速度公式求出撤去F时物体的速度大小;撤去拉力后物体先做匀减速直线运动至速度减为零,利用牛顿第二定律和速度公式结合求时间时间![]() ;(3)由位移公式求得物体从撤去到滑到最高点的过程运动的位移,再研究下滑过程,利用牛顿第二定律和位移公式结合求解.
;(3)由位移公式求得物体从撤去到滑到最高点的过程运动的位移,再研究下滑过程,利用牛顿第二定律和位移公式结合求解.
(1)物块在时间![]() 内沿斜面匀加速上滑,设加速度大小为
内沿斜面匀加速上滑,设加速度大小为![]()
由牛顿第二定律有: ![]()
解得: ![]()
在这段吋间内物块上滑的距离为: ![]()
(2)经时间![]() 物块的速度大小为:
物块的速度大小为: ![]()
接着物块沿斜面匀减速上滑,设加速度大小为![]()
由牛顿第二定律有: ![]()
解得: ![]()
根据速度公式有: ![]()
解得![]()
(2)物块在时间![]() 内上滑的距离为:
内上滑的距离为: ![]()
物块沿斜面下滑的时间为: ![]()
设物块沿斜面下滑的加速度大小为![]()
由牛顿第二定律有: ![]()
解得: ![]()
物块在时间![]() 内沿斜面下滑的距离为:
内沿斜面下滑的距离为: ![]()
故: ![]()

练习册系列答案
相关题目