题目内容
(12分)如图所示,微粒A位于一定高度处,其质量m = 1×10-4kg、带电荷量q =" +" 1×10-6C,塑料长方体空心盒子B位于水平地面上,与地面间的动摩擦因数μ = 0.1。B上表面的下方存在着竖直向上的匀强电场,场强大小E = 2×103N/C,B上表面的上方存在着竖直向下的匀强电场,场强大小为 E。B上表面开有一系列略大于A的小孔,孔间距满足一定的关系,使得A进出B的过程中始终不与B接触。当A以υ1 = 1m/s的速度从孔1竖直向下进入B的瞬间,B恰以υ2 = 0.6m/s的速度向右滑行。设B足够长、足够高且上表面的厚度忽略不计,取g = 10m/s2,A恰能顺次从各个小孔进出B 。试求:
E。B上表面开有一系列略大于A的小孔,孔间距满足一定的关系,使得A进出B的过程中始终不与B接触。当A以υ1 = 1m/s的速度从孔1竖直向下进入B的瞬间,B恰以υ2 = 0.6m/s的速度向右滑行。设B足够长、足够高且上表面的厚度忽略不计,取g = 10m/s2,A恰能顺次从各个小孔进出B 。试求:
(1)从A第一次进入B至B停止运动的过程中,B通过的总路程s;
(2)B上至少要开多少个小孔,才能保证A始终不与B接触;
(3)从右到左,B上表面各相邻小孔之间的距离分别为多大?
(1)0.18m;(2)5;(3)0.1m;0.035m;0.04m;0.005m;
解析试题分析:(1)A在B内、外运动时,B的加速度大小:
a = =" μg" =" 1" m/s2 (1分)
=" μg" =" 1" m/s2 (1分)
B全过程做匀减速直线运动,所以通过的总路程
s = 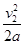 = 0.18m (2分)
= 0.18m (2分)
(2)A第二次进入B之前,在B内运动的加速度大小:
a1 = 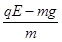 =" 10" m/s2
=" 10" m/s2
运动的时间: t1 =" 2" × 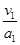 = 0.2s (1分)
= 0.2s (1分)
在B外运动的加速度大小:a2 = 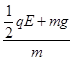 =" 20" m/s2
=" 20" m/s2
运动的时间:t2 =" 2" ×  = 0.1s (1分)
= 0.1s (1分)
A从第一次进入B到第二次进入B的时间:
t = t1 + t2 = 0.3s (1分)
A运动一个周期B减少的速度为:
△υ =" at=" 0.3m/s (1分)
从小球第一次进入B到B停下,A运动的周期数为:
n =  =
= 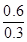 = 2
= 2
故要保证小球始终不与B相碰,B上的小孔个数至少为:
2n + 1 = 5 (1分)
(3)由于B向右做匀减速直线运动,经0.6s速度减为零,由逆向思维可知,B向左做初速度为零的匀加速直线运动了0.6s,每经过0.1s,其位移大小之比为1∶3∶5∶7∶9∶11,共有(1 + 3 + 5 + 7 + 9 + 11)份即36份,所以,从右到左,B上表面各相邻小孔之间的距离分别为
S1= 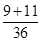 s = 0.1m (1分)
s = 0.1m (1分)
S2= s = 0.035m (1分)
s = 0.035m (1分)
S3=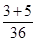 s = 0.04m (1分)
s = 0.04m (1分)
S4=  s = 0.005m (1分)
s = 0.005m (1分)
考点:带电粒子在电场中的运动、匀变速直线运动公式、牛顿第二定律

 .求:
.求: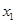 ;
;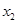 .
. 时再做匀速运动,进站前开始匀减速制动,在到达车站时刚好停住。公共汽车在每个车站停车时间均为
时再做匀速运动,进站前开始匀减速制动,在到达车站时刚好停住。公共汽车在每个车站停车时间均为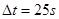 。然后以同样的方式运行至下一站。已知公共汽车在加速启动和减速制动时加速度大小都为
。然后以同样的方式运行至下一站。已知公共汽车在加速启动和减速制动时加速度大小都为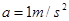 ,而所有相邻车站间的行程都为
,而所有相邻车站间的行程都为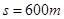 ,有一次当公共汽车刚刚抵达某一个车站时,一辆电动车已经过该车站向前运动了
,有一次当公共汽车刚刚抵达某一个车站时,一辆电动车已经过该车站向前运动了 ,已知该电动车速度大小恒定为
,已知该电动车速度大小恒定为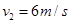 ,而且行进路线、方向与公共汽车完全相同,不考虑其他交通状况的影响,试求:
,而且行进路线、方向与公共汽车完全相同,不考虑其他交通状况的影响,试求: