题目内容
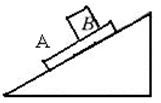
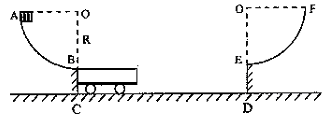
（09年聊城一中期末）（13分）在如图所示的装置中，两个光滑的定滑轮的半径很小，表面粗糙的斜面固定在地面上，斜面的倾角为θ＝30°。用一根跨过定滑轮的细绳连接甲、乙两物体，把甲物体放在斜面上且连线与斜面平行，把乙物体悬在空中，并使悬线拉直且偏离竖直方向
＝60°．现同时释放甲、乙两物体，乙物体将在竖直平面内振动，当乙物体运动经过最高点和最低点时，甲物体在斜面上均恰好未滑动．已知乙物体的质量为m＝1，若取重力加速度g＝10m/s2。试求：
（1）乙物体运动经过最高点和最低点时悬绳的拉力；
（2）甲物体的质量及斜面对甲物体的最大静摩擦力。
解析：（1）设乙物体运动到最高点时，绳子上的弹力为T1，
对乙物体 
＝5N
当乙物体运动到最低点时，绳子上的弹力为T2
对乙物体由机械能守恒定律： 
又由牛顿第二定律： 
得：
＝20N
（2）设甲物体的质量为M，所受的最大静摩擦力为f ，
乙在最高点时甲物体恰好不下滑，有：
乙在最低点时甲物体恰好不上滑，有： 
可解得： 
练习册系列答案
相关题目
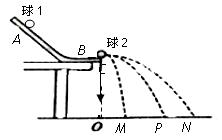
，其中v10和v20分别是碰撞前两物体的速度，v1和v2分别是碰撞后两物体的速度。弹性碰撞的恢复系数e＝1，非弹性碰撞的e＜1。某同学借用验证动量守恒定律的实验装置（如图所示）验证弹性碰撞的恢复系数是否为1，实验中使用半径相等的钢质小球1和2，（它们之间的碰撞可近似视为弹性碰撞），且小球1的质量大于小球2的质量。
时，木板的动量为 ；当B在木板上动量为 
，木板的动量为 。