题目内容
11.滑板运动是深受年轻人喜爱的一种极限运动.一种U型池的滑板运动场地截面示意图如图所示,场地由两个完全相同的$\frac{1}{4}$圆弧滑道AB、CD和水平滑道BC构成,圆弧滑道的半径R=4.25m,B、C分别为圆弧滑道的最低点,B、C间的距离s=8.0m.运动员从A点出发,通过AB、BC滑道,冲向CD滑道,到达圆弧滑道的最高位置D后竖直向上腾空跃起,在空中做出翻身、旋转等动作,然后再落回D点.假设某次运动中运动员经过水平滑道B点时水平向右的速度v0=17m/s,运动员从B点运动到C点所用时间t=0.5s,从D点跃起时的速度vD=8.0m/s.设运动员连同滑板的质量m=50kg,忽略空气阻力的影响,假定BC间阻力不变,重力加速度g取l0m/s2.求: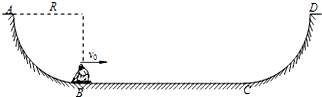
(1)运动员以v0速度经过B点时地面对运动员的支持力大小;
(2)运动员从C点到D点运动的过程中需要克服阻力所做的功;
(3)若运动员从D点返回需要在BC段通过蹬地做功才能重新到A点,某同学想计算此运动员需要通过蹬地做多少功W 才能恰好回到A点,其立式分析如下:W-WfDC-WfCB-WfBA=0-$\frac{1}{2}$mvD2,其中WfCB等于从B到C过程动能减少量,即WfCB=$\frac{1}{2}$mvC2-$\frac{1}{2}$mvB2;WfDC和WfBA的数值等于(2)问中C点到D点运动的过程中需要克服摩擦阻力所做的功的大小.这位同学的分析正确吗?若正确请计算W 的大小;若不正确,请简要说明理由.
分析 (1)在B点做圆周运动,根据牛顿第二定律求的相互作用力;
(2)在BC段运动员做匀减速运动,根据运动规律求得运动在C点的速度,再根据动能定理求得从C至D过程中克服摩擦力做的功;
(3)答案不正触,摩擦力的大小与正压力有关,而在圆弧面上由于运动速度不同,摩擦力的大小也不同,故摩擦力做的功不同,所以此分析是错误的
解答 解:(1)在B点做圆周运动,有牛顿第二定律可得${F}_{N}-mg=\frac{{mv}_{0}^{2}}{R}$
解得FN=3900N
(2)从B到C为匀变速运动,根据匀变速直线运动的平均速度公式有:$\overline{{v}_{BC}}=\frac{s}{t}=\frac{{v}_{B}+{v}_{C}}{2}$
所以可得运动员经过C点时的速度:vc=$2\frac{s}{t}-{v}_{B}=2×\frac{8}{0.5}-17m/s=15m/s$
从C到D令克服摩擦力做功为Wf,则根据动能定理有:
$-Wf-mgR=\frac{1}{2}{mv}_{D}^{2}-\frac{1}{2}{mv}_{C}^{2}$
带入数据得克服摩擦阻力所做的功:Wf=1900J;
(3)若运动员从D点返回需要在BC段通过蹬地做功才能重新到A点,某同学想计算此运动员需要通过蹬地做多少功W 才能恰好回到A点,其列式分析如下:W-WfDC-WfCB-WfBA=0-$\frac{1}{2}$mvD2其中WfCB大小等于从B到C过程动能减少量,即WfCB=$\frac{1}{2}$mvC2-$\frac{1}{2}$mvB2;WfCD和WfBA等于(2)小题中C点到D点运动的过程中克服摩擦阻力所做的功的大小.这位同学的分析不正确,D到C,B到A过程与C到D比较,速度不同,根据向心力公式,支持力不同,摩擦力也不同,则摩擦力做功不同
答:(1)运动员以v0速度经过B点时地面对运动员的支持力大小为3900N;
(2)运动员从C点到D点运动的过程中需要克服阻力所做的功为1900J
(3)分析不正确
因为C到D和D到C速度不一样,滑道对运动员的支持力不样,克服摩擦力做功不一样.
点评 本题综合考查了动能定理、牛顿第二定律,涉及到圆周运动运动,匀变速直线运动,竖直上抛运动,综合性较强,难度中等

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | 波峰与波谷相遇处质点离开平衡位置的位移始终为|A1-A2| | |
| B. | 波峰与波峰相遇处质点离开平衡位置的位移始终为A1+A2 | |
| C. | 波峰与波谷相遇处质点的位移总是小于波峰与波峰相遇处质点的位移 | |
| D. | 波峰与波峰相遇处质点的振幅一定大于波峰与波谷相遇处质点的振幅 |
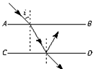 置于空气中的厚玻璃板,AB、CD分别是玻璃板的上、下表面,且AB∥CD,光线经AB表面射向玻璃砖时,折射光线射到CD表面时,下列说法正确的是?( )
置于空气中的厚玻璃板,AB、CD分别是玻璃板的上、下表面,且AB∥CD,光线经AB表面射向玻璃砖时,折射光线射到CD表面时,下列说法正确的是?( )| A. | 不可能发生全反射? | |
| B. | 有可能发生全反射? | |
| C. | 只要入射角i足够大就能发生全反射? | |
| D. | 不知玻璃折射率,无法判断? |
| A. | 线圈中磁通量变化越大,线圈中产生的感应电动势一定越大 | |
| B. | 线圈中磁通量越大,线圈中产的感应电动势一定越大 | |
| C. | 线圈放在磁场越强的位置,线圈中产生的感应电动势一定越大 | |
| D. | 线圈中磁通量变化越快,线圈中产生的感应电动势越大 |
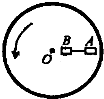 如图所示,在绕过盘心O的竖直轴匀速转动的水平盘上,沿半径方向放着用细线相连 的质量相等的两个物体A和B,它们与盘面间的动摩擦因数相同,当转速刚好使两个物体要滑动而未滑动时,烧断细线,则两个物体的运动情况是( )
如图所示,在绕过盘心O的竖直轴匀速转动的水平盘上,沿半径方向放着用细线相连 的质量相等的两个物体A和B,它们与盘面间的动摩擦因数相同,当转速刚好使两个物体要滑动而未滑动时,烧断细线,则两个物体的运动情况是( )| A. | 两物体均沿切线方向滑动 | |
| B. | 两物体均沿半径方向滑动,离圆盘圆心越来越远 | |
| C. | 两物体仍随圆盘一起做圆周运动,不发生滑动 | |
| D. | 物体B仍随圆盘一起做圆周运动,物体A发生滑动 |
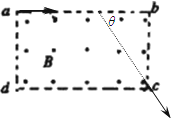 如图所示,矩形abcd范围内有垂直于纸面向外的匀强磁场,磁感应强度大小为B,ab的长度为L=$\frac{\sqrt{3}mv}{2qB}$,现有比荷为$\frac{q}{m}$的正离子从a点沿ab方向射入磁场,刚好从C点飞出,不计正离子的重力.求:
如图所示,矩形abcd范围内有垂直于纸面向外的匀强磁场,磁感应强度大小为B,ab的长度为L=$\frac{\sqrt{3}mv}{2qB}$,现有比荷为$\frac{q}{m}$的正离子从a点沿ab方向射入磁场,刚好从C点飞出,不计正离子的重力.求: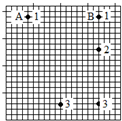 小球A从桌边水平抛出,当它恰好离开桌边缘时小球B从同样高度处自由下落,频闪照相仪拍到了A球和B球下落过程的三个位置,图中A球的第2个位置未画出.已知背景的方格纸每小格的边长为2.5cm,g取10m/s2.
小球A从桌边水平抛出,当它恰好离开桌边缘时小球B从同样高度处自由下落,频闪照相仪拍到了A球和B球下落过程的三个位置,图中A球的第2个位置未画出.已知背景的方格纸每小格的边长为2.5cm,g取10m/s2.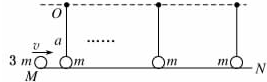
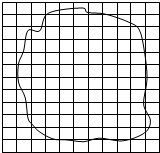 在“用油膜法估测分子的大小”实验中,将4mL的纯油酸溶液滴入20L无水酒精溶液中充分混合.注射器中1mL的上述混合溶液可分50滴均匀滴出,将其中的1滴滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,在玻璃板上描出油膜的轮廓,随后把玻璃板放在坐标纸上,其形状如图所示,坐标纸上正方形小方格的边长为10mm.试解答下列问题,结果均取一位有效数字.
在“用油膜法估测分子的大小”实验中,将4mL的纯油酸溶液滴入20L无水酒精溶液中充分混合.注射器中1mL的上述混合溶液可分50滴均匀滴出,将其中的1滴滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,在玻璃板上描出油膜的轮廓,随后把玻璃板放在坐标纸上,其形状如图所示,坐标纸上正方形小方格的边长为10mm.试解答下列问题,结果均取一位有效数字.