题目内容
16.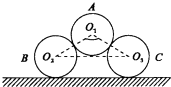 如图所示,三个粗细均匀完全相同的圆木A、B、C堆放在水平地面上,处于静止状态,每个圆木的质量为m,截面的半径为R,三个截面圆心连线构成的等腰三角形的顶角∠O1=120°,若在地面上的两个圆木刚好要滑动,设最大静摩擦力等于滑动摩擦力,不考虑圆木之间的摩擦,重力加速度为g,则( )
如图所示,三个粗细均匀完全相同的圆木A、B、C堆放在水平地面上,处于静止状态,每个圆木的质量为m,截面的半径为R,三个截面圆心连线构成的等腰三角形的顶角∠O1=120°,若在地面上的两个圆木刚好要滑动,设最大静摩擦力等于滑动摩擦力,不考虑圆木之间的摩擦,重力加速度为g,则( )| A. | 圆木间的弹力为$\frac{1}{2}$mg | |
| B. | 地面上的每个圆木对地面的压力为$\frac{3}{2}$mg | |
| C. | 地面上的每个圆木受到地面的作用力为$\frac{3}{2}$mg | |
| D. | 地面与圆木间的动摩擦因数为$\frac{\sqrt{3}}{2}$ |
分析 对A进行受力分析,A处于平衡状态,合力为零,根据平衡条件求出A、B之间的弹力大小,对B受力分析,根据B处于静止状态分析B与地面间是否有摩擦力,根据对称性可知,BC的受到的摩擦力大小相等,方向相反,对B受力分析求解摩擦力,B受到的是静摩擦力,根据静摩擦力小于等于滑动摩擦力求解动摩擦因数.
解答 解:A、对A进行受力分析,如图所示:
A处于平衡状态,合力为零,则有:
${N}_{2}cos\frac{θ}{2}=\frac{1}{2}mg$
解得:${{N}_{1}=N}_{2}=\frac{\frac{1}{2}mg}{cos60°}=mg$,故A错误;
B、对整体受力分析,受到重力、地面的支持力、B受到的向右的摩擦力和C受到的向左的摩擦力,由对称性可知,竖直方向:${N}_{B}={N}_{C}=\frac{3}{2}mg$,故B正确;
C、对C研究,地面对B的作用力等于地面对C的支持力与地面对B摩擦力的合力,大于$\frac{3}{2}$mg,故C错误;
D、根据对称性可知,C受到的摩擦力与B受到的摩擦力大小相等,
对C根据平衡条件得:
f=${N}_{2}sin60°=mg×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}mg$,所以地面对C的摩擦力大小为$\frac{\sqrt{3}}{2}$mg,
根据摩擦力的公式:f=μFN
所以:$μ=\frac{f}{{F}_{N}}=\frac{\frac{\sqrt{3}}{2}mg}{\frac{3}{2}mg}=\frac{\sqrt{3}}{3}$.故D错误.
故选:B
点评 对A进行受力分析,A处于平衡状态,合力为零,根据平衡条件求出A、B之间的弹力大小,对B受力分析,根据B处于静止状态分析B与地面间是否有摩擦力,根据对称性可知,BC的受到的摩擦力大小相等,方向相反,对B受力分析求解摩擦力,B受到的是静摩擦力,根据静摩擦力小于等于滑动摩擦力求解动摩擦因数的范围.

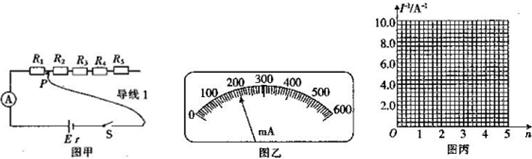
电流表A,阻值均为2.5 的定值电阻R1、R2、R3、R4、R5;开关S1一端连有鳄鱼夹P的导线1,其他导线若干.实验步骤如下:
①将鳄鱼夹P接在R1 右侧,仅使 R1串人电路闭合开关S,记录电流表的示数I;②改变鳄鱼夹P的位置,使鳄鱼夹P分别接在R2、R3、R4、R5 的右侧,记下电流表的示数I;③以$\frac{1}{I}$为纵坐标,接人电路中定值电阻n的个数为横坐标,作$\frac{1}{I}$-n图线(用直线拟合);④求出直线的斜率k和在纵轴上的截距b
回答下列问题:
(1)分别用E和r表示电源的电动势和内阻,则$\frac{1}{I}$与n的关系式为$\frac{1}{I}$=$\frac{R}{E}$n+$\frac{r}{E}$
(2)实验得到的部分数据如表所示,其中电阻n=3时电流表的示数如图乙所示,读出数据,完成表:①0.192②0.521
| n | 1 | 2 | 3 | 4 | 5 |
| I/A | 0.536 | 0.283 | ① | 0.146 | 0.117 |
| I-1/A-1 | 1.87 | 3.53 | ② | 6.87 | 8.53 |
(4)根据图线求得电源电动势E=1.5V,内阻r=0.3Ω.
 如图所示,在匀强磁场中匀速转动的单匝矩形线圈的周期为T=0.02s,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A,那么( )
如图所示,在匀强磁场中匀速转动的单匝矩形线圈的周期为T=0.02s,转轴O1O2垂直于磁场方向,线圈电阻为2Ω.从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1A,那么( )| A. | 线圈中感应电流的有效值为2A | |
| B. | 线圈消耗的电功率为8W | |
| C. | 任意时刻线圈中的感应电动势为e=4cos100πtV | |
| D. | 任意时刻穿过线圈的磁通量为Φ=$\frac{0.02}{π}$sin100πtWb |
| A. | 点电荷周围的电场可视为匀强电场 | |
| B. | 平行板电容器之间的电场除边缘外可视为匀强电场 | |
| C. | 直线电流周围的磁场可视为匀强磁场 | |
| D. | 环形电流周围的磁场可视为匀强磁场 |
| A. | 在${\;}_1^2H+{\;}_1^3H→{\;}_2^4{H_e}+x$核反应中,x是质子,核反应放出的能量等于${\;}_1^2H$和${\;}_1^3H$的质量和减去${\;}_2^4{H_e}$和x的质量和,再乘c2(c表示光速) | |
| B. | 卫星可以在大于地球半径的任意圆轨道上运动,电子也可以在大于基态轨道半径的任意圆轨道上运动 | |
| C. | 分别用绿光和紫光照射同一金属表面都能发生光电效应,逸出的光电子的动能可能相等 | |
| D. | 随着温度的升高,一方面各种波长的辐射强度都有增加,另一方面辐射强度的极大值向波长较短的方向移动 | |
| E. | 在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此光子散射后波长变长 | |
| F. | 在α粒子散射实验中,当在α粒子最接近原子核时,α粒子与金原子核组成的系统能量最小 |
 如图所示,用一根细线一端固定在一光滑斜面顶上,另一端系一可视为质点的小球m,设线的张力大小为F、斜面对小球的支持力大小为FN,光滑斜面在外力作用下向右做加速度增大的加速运动,(细线不会被拉断)则F和FN随α变化的情况是( )
如图所示,用一根细线一端固定在一光滑斜面顶上,另一端系一可视为质点的小球m,设线的张力大小为F、斜面对小球的支持力大小为FN,光滑斜面在外力作用下向右做加速度增大的加速运动,(细线不会被拉断)则F和FN随α变化的情况是( )| A. | F一直减小 | B. | F先增大后减小 | C. | FN一直增大 | D. | FN先减小后不变 |


 法国人劳伦特•菲舍尔在澳大利亚伯斯的冒险世界进行了超高空特技跳水表演,他从30m高的塔上跳下,假设他以5m/s的初速度竖直向下离开塔顶,并准确地落入水池中.已知:他在空气中运行时,空气对他的阻力是他重力的0.2倍;水池深度为10.1m.求:(菲舍尔可视为质点,g取10m/s2)
法国人劳伦特•菲舍尔在澳大利亚伯斯的冒险世界进行了超高空特技跳水表演,他从30m高的塔上跳下,假设他以5m/s的初速度竖直向下离开塔顶,并准确地落入水池中.已知:他在空气中运行时,空气对他的阻力是他重力的0.2倍;水池深度为10.1m.求:(菲舍尔可视为质点,g取10m/s2)