题目内容
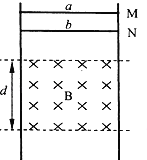
【题目】如图所示,两根电阻忽略不计、互相平行的光滑金属导轨竖直放置,相距L=1m,在水平虚线间有与导轨所在平面垂直的匀强磁场,磁感应强度B=0.5T,磁场区域的高度d=1m,导体棒a的质量ma=0.2kg、电阻Ra=1Ω;导体棒b的质量mb=0.1kg、电阻Rb=1.5Ω.它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动,b匀速穿过磁场区域,且当b刚穿出磁场时a正好进入磁场,重力加速度g=10m/s2,不计a、b棒之间的相互作用,导体棒始终与导轨垂直且与导轨接触良好,求:
(1)b棒穿过磁场区域过程中克服安培力所做的功;
(2)a棒刚进入磁场时两端的电势差;
(3)保持a棒以进入时的加速度做匀变速运动,对a棒施加的外力随时间的变化关系.
【答案】(1)b棒穿过磁场区域过程中克服安培力所做的功为1J;(2)a棒刚进入磁场时两端的电势差为3.3V;
(3)保持a棒以进入时的加速度做匀变速运动,对a棒施加的外力随时间的变化关系为F=0.45t﹣1.1.
【解析】
(1)b在磁场中匀速运动,其安培力等于重力,根据重力做功情况求出b棒克服安培力分别做的功.
(2)b进入磁场做匀速直线运动,受重力和安培力平衡,根据平衡条件,结合闭合电路欧姆定律和切割产生感应电动势大小公式,求出b做匀速直线运动的速度大小.a、b都在磁场外运动时,速度总是相等,b棒进入磁场后,a棒继续加速运动而进入磁场,根据运动学速度时间公式求解出a进入磁场时的速度大小,由E=BLv求出a棒产生的感应电动势,即可求得a棒刚进入磁场时两端的电势差.
(3)根据牛顿第二定律求出a棒刚进入磁场时的加速度,再根据牛顿第二定律求出保持a棒以进入时的加速度做匀变速运动时外力与时间的关系式.
(1)b棒穿过磁场做匀速运动,安培力等于重力,则有:BI1L=mbg,
克服安培力做功为:W=BI1Ld=mbgd=0.1×10×1=1J
(2)b棒在磁场中匀速运动的速度为v1,重力和安培力平衡,根据平衡条件,结合闭合电路欧姆定律得:
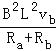 =mbg,vb=
=mbg,vb=![]() =
=![]() =10m/s,
=10m/s,
b棒在磁场中匀速运动的时间为t1,d=vbt1,t1=![]() =
=![]() =0.1s,a、b都在磁场外运动时,速度总是相等的,b棒进入磁场后,a棒继续加速t1时间而进入磁场,a棒进入磁场的速度为va,va=vb+gt1=10+10×0.1=11m/s.
=0.1s,a、b都在磁场外运动时,速度总是相等的,b棒进入磁场后,a棒继续加速t1时间而进入磁场,a棒进入磁场的速度为va,va=vb+gt1=10+10×0.1=11m/s.
电动势为:E=BLva=0.5×1×11=5.5V,a棒两端的电势差即为路端电压为:U=![]() =
=![]() =3.3V.
=3.3V.
(3)a棒刚进入磁场时的加速度为a,根据牛顿第二定律得:mag﹣BI2L=maa,
a=g﹣![]() =g﹣
=g﹣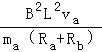 =10﹣
=10﹣![]() =4.5m/s2,
=4.5m/s2,
要保持加速度不变,加外力F,根据牛顿第二定律得:F+mag﹣BIL=maa
得:F=![]() t=
t=![]() ×t=0.45t﹣1.1.
×t=0.45t﹣1.1.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案