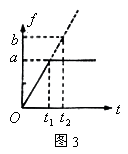题目内容
物体A的质量m="l" kg，静止在光滑水平面上的平板车B的质量为M=0．5kg，平板车长为L=1m。某时刻A以vo=4m／s向右的初速度滑上平板车B的上表面，在A滑上平板车B的同时，给平板车B施加一个水平向右的拉力。忽略物体A的大小，已知A与平板车B之间的动摩擦因数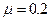
，取重力加速度g=10m/s2．试求：
（1）若F=5N，物体A在平板车上运动时相对平板车向前滑行的最大距离；
（2）如果要使A不至于从平板车B上滑落，拉力F大小应满足的条件．
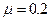，取重力加速度g=10m/s2．试求：（1）若F=5N，物体A在平板车上运动时相对平板车向前滑行的最大距离；
（2）如果要使A不至于从平板车B上滑落，拉力F大小应满足的条件．
（1）0.5m （2）1N≤F≤3N
（1）物体A滑上平板车B以后，物体作匀减速运动，平板车作匀加速运动，两者速度相同时,物体A在平板车上相对小车向前滑行的距离最大。
由牛顿第二定律，对物体A有：µmg =maA 得aA=µg="2" m/s2
对平板车B有：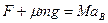
①
得：aB="14" m/s2
两者速度相同时，有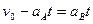
得：t="0.25s " （2分）
此过程：A滑行距离：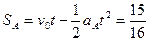
m
B滑行距离：
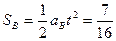m
此时物体A相对小车向前滑行的距离最大：△s= SA- SB="0.5m "
（2）物体A不从车右端滑落的临界条件是A到达B的右端时，A、B具有共同的速度v1，
则：
………②
又：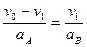
……………③
由② ③式，可得：aB="6 " m/s2
代入①式得： F="M" aB—µmg="1" N
若F＜1N，则A滑到B的右端时，速度仍大于B的速度，于是将从小车B的右端滑落。
当F较大时，在A到达B的右端之前，就与B具有相同的速度，之后，A必须相对B静止，才不会从B的左端滑落。
即有：F=（M+m）am，
µm1g =m1am
解之得：F＝3N
若F大于3N，A就会从小车B的左端滑下。
综上：力F应满足的条件是： 1N≤F≤3N
由牛顿第二定律，对物体A有：µmg =maA 得aA=µg="2" m/s2
对平板车B有：
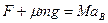①得：aB="14" m/s2
两者速度相同时，有
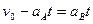
得：t="0.25s " （2分）
此过程：A滑行距离：
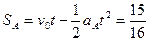m B滑行距离：
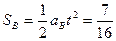m 此时物体A相对小车向前滑行的距离最大：△s= SA- SB="0.5m "
（2）物体A不从车右端滑落的临界条件是A到达B的右端时，A、B具有共同的速度v1，
则：
………② 又：
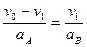……………③ 由② ③式，可得：aB="6 " m/s2
代入①式得： F="M" aB—µmg="1" N
若F＜1N，则A滑到B的右端时，速度仍大于B的速度，于是将从小车B的右端滑落。
当F较大时，在A到达B的右端之前，就与B具有相同的速度，之后，A必须相对B静止，才不会从B的左端滑落。
即有：F=（M+m）am，
µm1g =m1am
解之得：F＝3N
若F大于3N，A就会从小车B的左端滑下。
综上：力F应满足的条件是： 1N≤F≤3N
练习册系列答案
相关题目
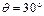、足够长的斜面上分别固定着两个物体A．B，相距L=0.2m，它们的质量mA=mB=1kg，与斜面间的动摩擦因数分别为
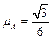和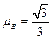
．在t=0时刻同时撤去固定两物体的外力后，A物体将沿斜面向下运动，并与B物体发生连续碰撞(碰撞时间极短，忽略不计)，每次碰后两物体交换速度．g取10m/s2．求：
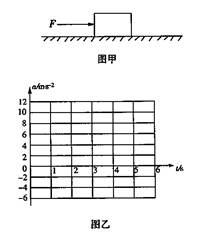
0.10，现对木板施加水平向右的拉力F=10N，为使木板能从物体下方被抽出，此拉力作用不得少于多少时间? 
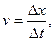“v—t”图象下的“面
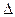x；加速度的定义为
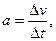则“a—t”图象下面的“面积”在数
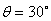，物体A和B的质量分别为
、
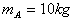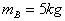。两者之间用质量可以不计的细绳相连。求：
，
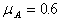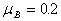时，两物体的加速度各为多大？绳的张力为多少？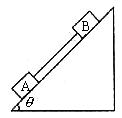
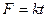（常量k>0）。设物块从
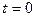时刻起由静止开始沿墙壁竖直向下滑动，物块与墙壁间的动摩擦因数为
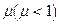，得到物块与竖直墙壁间的摩擦力f随时间t变化的图象，如图3所示，从图线可以得出（ ）
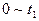时间内，物块在竖直方向做匀速直线运动