题目内容
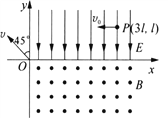
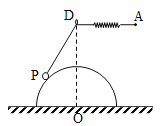
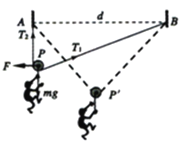
【题目】右图为特种兵过山谷的简化示意图，山谷的左侧为竖直陡崖,右侧是坡面为
的斜坡。将一根不可神长的细绳两端固定在相距d为20m的A、B两等高点。绳上挂一小滑轮P，战士们相互配合，沿着绳子滑到对面。如图所示，战士甲(图中未画出)水平拉住清轮，质量为50kg的战土乙吊在滑轮上，脚离地处于静止状态，此时AP竖直， 
,然后战士甲将滑轮由静止释放，战士乙即可滑到对面某处。不计滑轮大小、摩擦及空气阻力，也不计绳与滑轮的质量，重力加速度g取
， 
。
(1)求战士甲释放滑轮前对滑轮的水平拉力F；
(2)当战士乙运动到曲线的最低点附近时，可看做半径
的圆的一部分，求战士乙在最低点时绳的拉力；
(3)以A、B的中点O为坐标原点,水平线AB为x轴，竖直向上为y轴正方向，建立正交坐标系，求战士乙运动到右侧坡面的坐标。
【答案】（1）
（2）
（3）
【解析】解：（1）受力分析如图，根据共点力平衡条件得到：
联立解得： 
（2）
， 
，所以
是正三角形， 
在AB水平线下方
处，以
为零势能面， 
根据机械能守恒定律： 
由牛顿第二定律和圆周运动规律得到： 
联立解得： 
（2）由题意可得战士的运动轨迹为椭圆， 
，半短轴
，半长轴
椭圆方程为： 
设右侧坡面的轨迹方程为： 
将
代入得到： 
则右侧坡面的轨迹方程为： 
联立解得： 
解得： 
， 
后者不合题意舍去
练习册系列答案
相关题目
